7 Detección de comunidades
En esta parte consideramos algunos métodos de detección de comunidades, como una introducción a este tema amplio e importante.
Las redes sociales y otras comunmente tienen subgrupos de vértices o nodos tales que hay una gran cantidad de conexiones entre ellos y menos conexiones fuera de ese grupo, o comunidades que es posible identificar. Existen distintas definiciones y algoritmos útiles para hacer análisis de comunidades: algunas particionan los nodos en clusters (como algoritmos de clustering), algunos otros permiten identificar comunidades traslapadas.
Por ejemplo: en nuestra red personal de facebook o algo similar existen comunidades como familia, amigos de la secundaria o preparatoria, compañeros de trabajo, etc, y quizá algunos conocidos que no pertenecen a ninguna de estas comunidades. Naturalmente pertenecemos a todos estos grupos. Por otro lado, quizá si analizamos la red de retweets de un tema particular, podemos encontrar comunidades separadas (muchos retweets entre ellos, pocos retweets fuera del grupo) y cada persona se puede clasificar como de un “equipo”.
Ejemplo: red de club de karate
De la descripción en igraphdata de estos datos:
Social network between members of a university karate club, led by president John A. and karate instructor Mr. Hi (pseudonyms). The edge weights are the number of common activities the club members took part of. Zachary studied conflict and fission in this network, as the karate club was split into two separate clubs, after long disputes between two factions of the club, one led by John A., the other by Mr. Hi.
Hacemos cálculos y graficamos:
library(tidyverse)
library(tidygraph)
library(ggraph)
library(igraphdata)
data(karate)
karate_red <- karate %>% as_tbl_graph() %>%
activate(nodes) %>%
mutate(grado = centrality_eigen()) %>%
mutate(grupo = group_fast_greedy(weights = weight)) %>%
mutate(grupo = as.factor(grupo)) %>%
mutate(name = ifelse(str_detect(name, "Actor"), str_sub(name, 7, 10), name))ggraph(karate_red, layout = 'fr') +
geom_edge_link(aes(alpha = weight)) +
geom_node_point(aes(size = grado, colour = grupo)) +
geom_node_text(aes(label = name), repel = TRUE) +
theme_graph()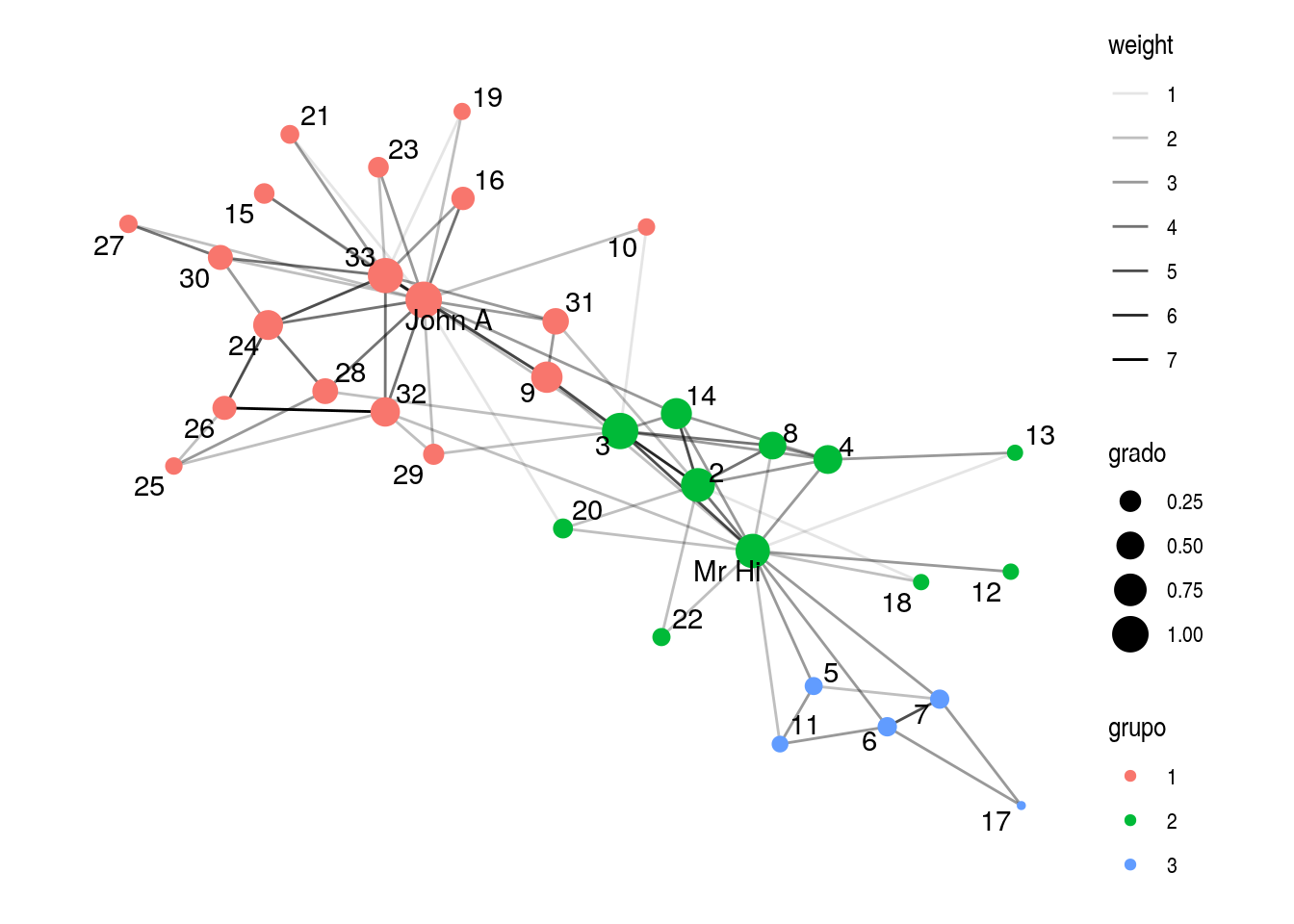
Este método identifica dos comunidades grandes, la de Mr Hi, la de John A, y otra más chica que está conectada solamente a la de Mr Hi. Nótese que las ligas entre elementos de la comunidad son densas dentro de la comunidad y menos densas hacia afuera, aunque hay unos individuos que están en las fronteras (como 3 y 9, por ejemplo).
¿Cómo encontrar estos módulos?
7.1 Modularidad
El concepto de modularidad es uno básico para intentar cuantificar qué tan buena o “cohesiva” es una separación de nodos en grupos.
Para definir esta cantidad, comenzamos con la matriz de adyacencia \(A\) de una gráfica no dirigida, y una agrupación de vértices en grupos.
Para empezar, notamos que el número total de aristas en la gráfica es
\[m = \frac{1}{2}\sum_{u,v} A_{u,v},\]
donde dividimos entre dos para no contar doble las aristas no dirigidas.
Ahora sea \(g(v)\) el grupo al que pertenece el vértice \(v\). Calculamos el número de aristas de aristas conectan elementos del mismo grupo:
\[\frac{1}{2}\sum_{u,v} A_{u, v} I(g(u), g(v))\]
nótese que un elemento de esta suma es igual a 0 o 1, y solo es igual a 1 cuando \(u\) y \(v\) están conectados y \(u\) y \(v\) pertenecen al mismo grupo (\(I(g,h)\) es la función indicadora de identidad, es decir vale 1 si \(g=h\) y 0 en otro caso).
Entonces la fracción de aristas del total de aristas que conecta vértices dentro del mismo grupo es
\[\frac{\sum_{u,v} A_{u, v} I(g(u), g(v))}{\sum_{u,v} A_{u, v}} = \frac{1}{2m}\sum_{u,v} A_{u, v} I(g(u), g(v))\]
donde \(m\) es el número de aristas. Esta cantidad va a ser grande para particiones “cohesivas”, que agrupan vértices en comunidades densas y chica en otro caso. En general, esta formulación también aplica a multigrafos, en cuyo caso puede \(A_{u,v}\) cuenta el número de aristas entre los nodos \(u\) y \(v\), y no solo vale 1 o 0.
Ejemplo
#funcion para graficar
graficar_red_nd <- function(dat_g, layout = "nicely", grupo, nombres = TRUE){
gg <- ggraph(dat_g %>% activate(nodes), layout = layout) +
geom_edge_link(alpha=0.2) +
geom_node_point(aes(colour = {{ grupo }}), size = 5) +
theme_graph(base_family = "sans")
if(nombres){
gg <- gg + geom_node_text(aes(label = nombre), size=5, repel = TRUE)
}
gg
}
aristas <- tibble(from = c(10, 10, 10, 10, 1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 11),
to = c(7, 8, 9, 1, 2, 3, 1, 5, 6, 4, 9, 7, 8, 5, 7))
grupos <- c(rep('a', 3), rep('b', 3), rep('c', 5))
ejemplo_mod_alta <- tbl_graph(
nodes = tibble(nombre = seq(1, 11, 1),
grupo = grupos),
edges = aristas, directed = FALSE)
set.seed(89)
graficar_red_nd(ejemplo_mod_alta, layout = "gem", grupo = grupo)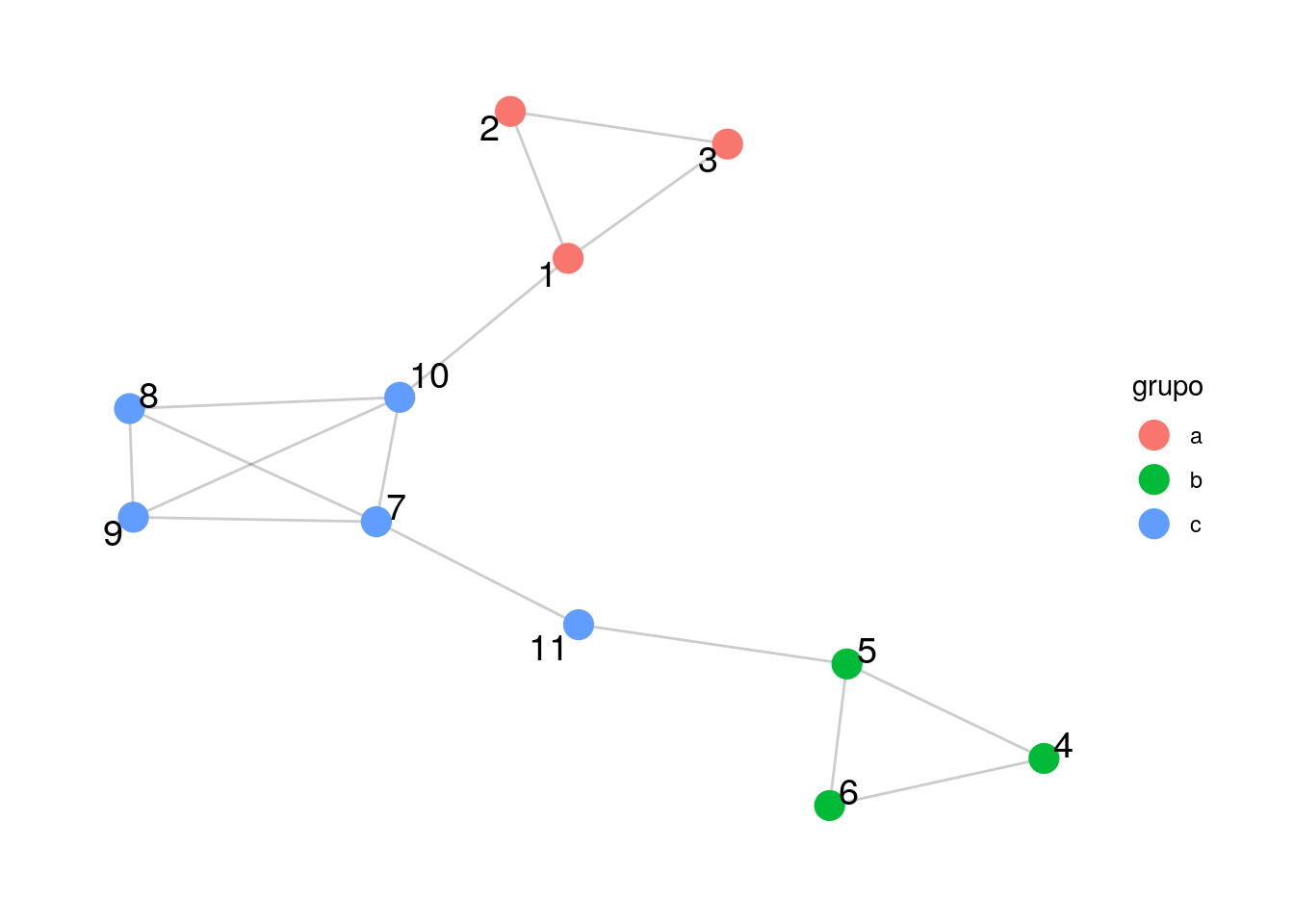
Cuya matriz de adyacencia \(A\) es
## 11 x 11 sparse Matrix of class "dgCMatrix"
##
## [1,] . 1 1 . . . . . . 1 .
## [2,] 1 . 1 . . . . . . . .
## [3,] 1 1 . . . . . . . . .
## [4,] . . . . 1 1 . . . . .
## [5,] . . . 1 . 1 . . . . 1
## [6,] . . . 1 1 . . . . . .
## [7,] . . . . . . . 1 1 1 1
## [8,] . . . . . . 1 . 1 1 .
## [9,] . . . . . . 1 1 . 1 .
## [10,] 1 . . . . . 1 1 1 . .
## [11,] . . . . 1 . 1 . . . .Nótense los bloques que se puede formar en la matriz de adyacencia (que es notable debido a cómo etiquetamos los nodos). Estas son las estructuras propias de una partición con modularidad alta.
Podemos calcular la fracción de aristas que conectan vértices del mismo grupo como sigue:
## 3 x 3 sparse Matrix of class "dgCMatrix"
##
## [1,] . 1 1
## [2,] 1 . 1
## [3,] 1 1 .g_b <- A[grupos == "b", grupos == "b"]
g_c <- A[grupos == "c", grupos == "c"]
frac_1 <- (sum(g_a) + sum(g_b) + sum(g_c)) / sum(A)
sprintf("Fracción de aristas dentro de mismo grupo: %0.3f", frac_1)## [1] "Fracción de aristas dentro de mismo grupo: 0.867"Ahora vemos un ejemplo de modularidad baja:
set.seed(12138)
ejemplo_mod_baja <- play_erdos_renyi(11, p = 0.4, directed = FALSE) %>%
activate(nodes) %>%
mutate(grupo = grupos, nombre = 1:11)
graficar_red_nd(ejemplo_mod_baja, layout = "gem", grupo = grupo)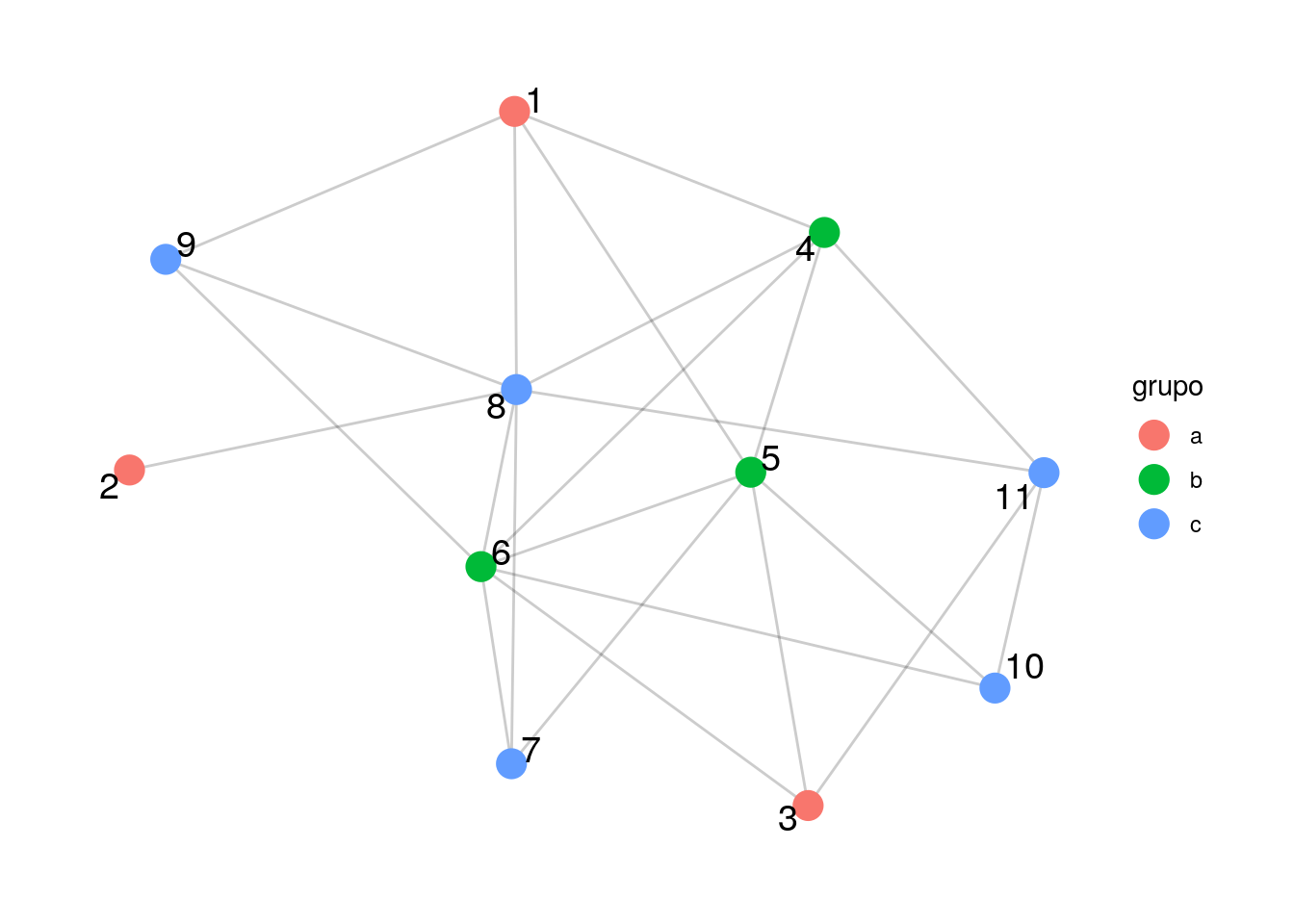
A <- igraph::get.adjacency(ejemplo_mod_baja)
g_a <- A[grupos == "a", grupos == "a"]
g_b <- A[grupos == "b", grupos == "b"]
g_c <- A[grupos == "c", grupos == "c"]
g_c## 5 x 5 sparse Matrix of class "dgCMatrix"
##
## [1,] . 1 . . .
## [2,] 1 . 1 . 1
## [3,] . 1 . . .
## [4,] . . . . 1
## [5,] . 1 . 1 .frac_2 <- (sum(g_a) + sum(g_b) + sum(g_c)) / sum(A)
sprintf("Fracción de aristas dentro de mismo grupo: %0.3f", frac_2)## [1] "Fracción de aristas dentro de mismo grupo: 0.304"Discusión: esta medida (fracción de aristas que conectan nodos en el mismo grupo) es una que podemos optimizar para buscar comunidades. Sin embargo, la modularidad no se define así, sino que consideramos una normalización adicional para hacerla más comparable de red a red. Nótese que:
- Redes con nodos con grados más altos naturalmente tienden a tener calificaciones de modularidad más altas que redes con menos aristas.
Una manera de normalizar es entonces considerar la modularidad comparada con lo que esperaríamos si, dejando fijo número de aristas y grados de vértices, las aristas se conectaran al azar. El proceso aleatorio es:
- Cortamos “a la mitad” todos las aristas de nuestra gráfica. Ahora conectamos mitades al azar.
- Calculamos la fracción de aristas que conectan nodos del mismo grupo.
Y calculamos el valor esperado de esta cantidad, que restamos de la fracción que obtuvimos para la red original. El resultado es la modularidad de nuestra red: la diferencia de fracción de nodos que conectan al mismo grupo menos lo que pasaría si conectáramos al azar las aristas.
Ahora podemos calcular directamente este valor esperado. Consideremos entonces dos aristas \(u\) y \(v\), que tienen grado \(k(u)\) y \(k(v)\) respectivamente, y sea \(m\) el número total de aristas. Entonces:
- Una media arista dada de \(u\) tiene probabilidad \(k(v)/(2m - 1)\) de quedar conectada a \(v\).
- El número de pruebas independientes es \(k(u)\), para cada media arista de \(u\).
- El valor esperado del número de conexiones entre \(u\) y \(v\) es entonces \(k(u)k(v)/(2m -1)\).
La idea es entonces promediar los valores del número de conexiones observadas menos las esperadas según el modelo aleatorio:
\[A_{u,v} - \frac{k(u)k(v)}{2m-1}\]
para obtener:
Observaciones:
- Típicamente se usa la división entre \(2m\) en lugar de \(2m-1\). Para gráficas no muy chicas esto no es muy importante.
- Si esta cantidad es cercana a cero, entonces la fracción de nodos intra-grupo es similar a la de una gráfica construida al azar.
- Esta cantidad puede ir de -0.5 a 1. Normalmente se consideran valores mayores a 0.3 como casos de modularidad fuerte, o de existencia de comunidades (ver Leskovec, Rajaraman, and Ullman (2014)).
- La modularidad puede entenderse entonces como sigue: es la fracción de aristas que conectan nodos del mismo grupo menos lo que esperaríamos si las aristas se distribuyeran al azar en la gráfica (respetando el grado de cada vértice).
Ejemplo
Para nuestro primer ejemplo la modularidad es
## [1] 0.4733333y para nuestro segundo ejemplo
## [1] -0.06805293Observación: la idea ahora es construir algoritmos para encontrar agrupaciones de modularidad máxima en una gráfica dada. Estas agrupaciones nos dan las comunidades si resultan tener modularidad alta.
7.2 Algoritmo miope (fast greedy)
Hay varios algoritmos para encontrar agrupaciones de modularidad alta en una gráfica dada. Consideramos el algoritmo fast greedy (Clauset, Newman, and Moore (2004), liga de arxiv), que está diseñado para redes posiblemente muy grandes.
Este algoritmo es similar a clustering jerárquico:
- Comenzamos con todos los vértices un su propia comunidad.
- Buscamos el par de comunidades (al principio vértices) que al unirse da el mayor incremento (o menor decremento) en \(Q\).
- Repetimos 2 hasta que todos los puntos están en una sola comunidad.
- Escogemos el número de comunidades que maximiza el valor del \(Q\) sobre todas las iteraciones.
Existen varias particularidades de este algoritmo que lo hacen rápido y apropiado para redes grandes (ver referencia. Otro método similar es el algoritmo de louvain, por ejemplo).
Ejemplo
library(igraphdata)
data(USairports)
airports <- as_tbl_graph(USairports)
# seleccionamos solo pasajeros
aristas <- airports %>%
activate(edges) %>%
select(to, from, Passengers) %>% as_tibble()
# agregar
aristas_agregados <- aristas %>%
filter(to != from) %>%
mutate(to_u = ifelse(to < from, to, from)) %>%
mutate(from_u = ifelse(to < from, from, to)) %>%
group_by(to_u, from_u) %>%
summarise(pax = sum(Passengers)) %>%
rename(to = to_u, from = from_u)
# nodos, y agregar estado
nodos <- airports %>% activate(nodes) %>%
as_tibble() %>%
separate(City, into = c('ciudad_nombre', 'estado'), sep = ', ')
# construir nueva red
rutas <- tbl_graph(nodes = nodos, edges = aristas_agregados,
directed = FALSE)
rutas## # A tbl_graph: 755 nodes and 4623 edges
## #
## # An undirected simple graph with 6 components
## #
## # Node Data: 755 x 4 (active)
## name ciudad_nombre estado Position
## <chr> <chr> <chr> <chr>
## 1 BGR Bangor ME N444827 W0684941
## 2 BOS Boston MA N422152 W0710019
## 3 ANC Anchorage AK N611028 W1495947
## 4 JFK New York NY N403823 W0734644
## 5 LAS Las Vegas NV N360449 W1150908
## 6 MIA Miami FL N254736 W0801726
## # … with 749 more rows
## #
## # Edge Data: 4,623 x 3
## from to pax
## <int> <int> <dbl>
## 1 1 2 8
## 2 1 4 481
## 3 1 6 7
## # … with 4,620 more rowslayout_rutas <- create_layout(rutas, layout = "graphopt", niter = 500)
ggraph(layout_rutas) +
geom_edge_link(aes(alpha = pax)) +
geom_node_point(aes(colour = factor(grupos))) +
theme_graph()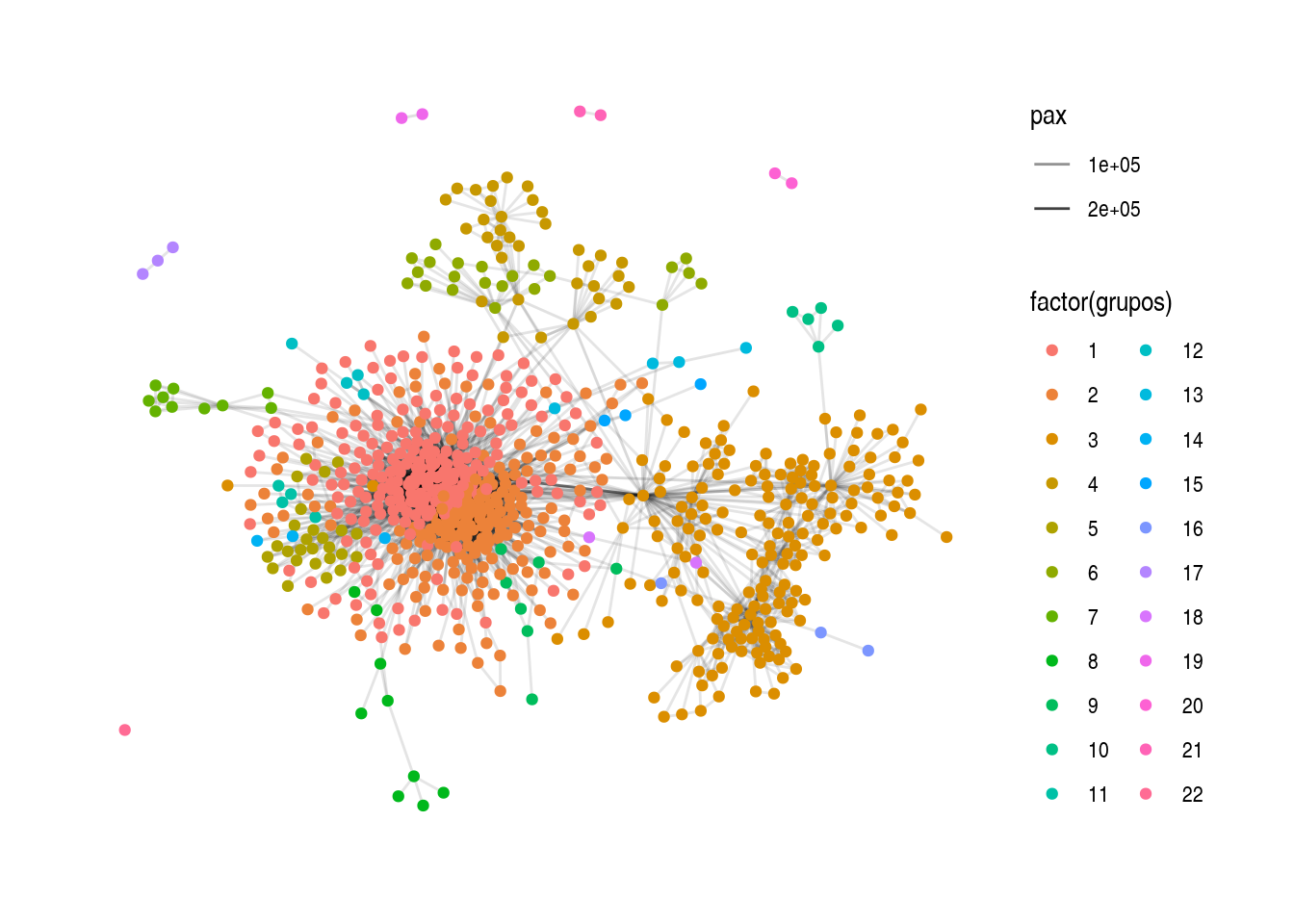
Podemos ver la modularidad
## [1] 0.4287122Podemos examinar algunas comunidades:
rutas_12 <- rutas %>% activate(nodes) %>% filter(grupos %in% c(1, 3, 4, 5, 6))
layout_rutas_12 <- create_layout(rutas_12, layout = "graphopt", niter = 2000)
ggraph(layout_rutas_12) +
geom_edge_link(aes(alpha = pax)) +
geom_node_point(aes(colour = factor(grupos))) +
theme_graph()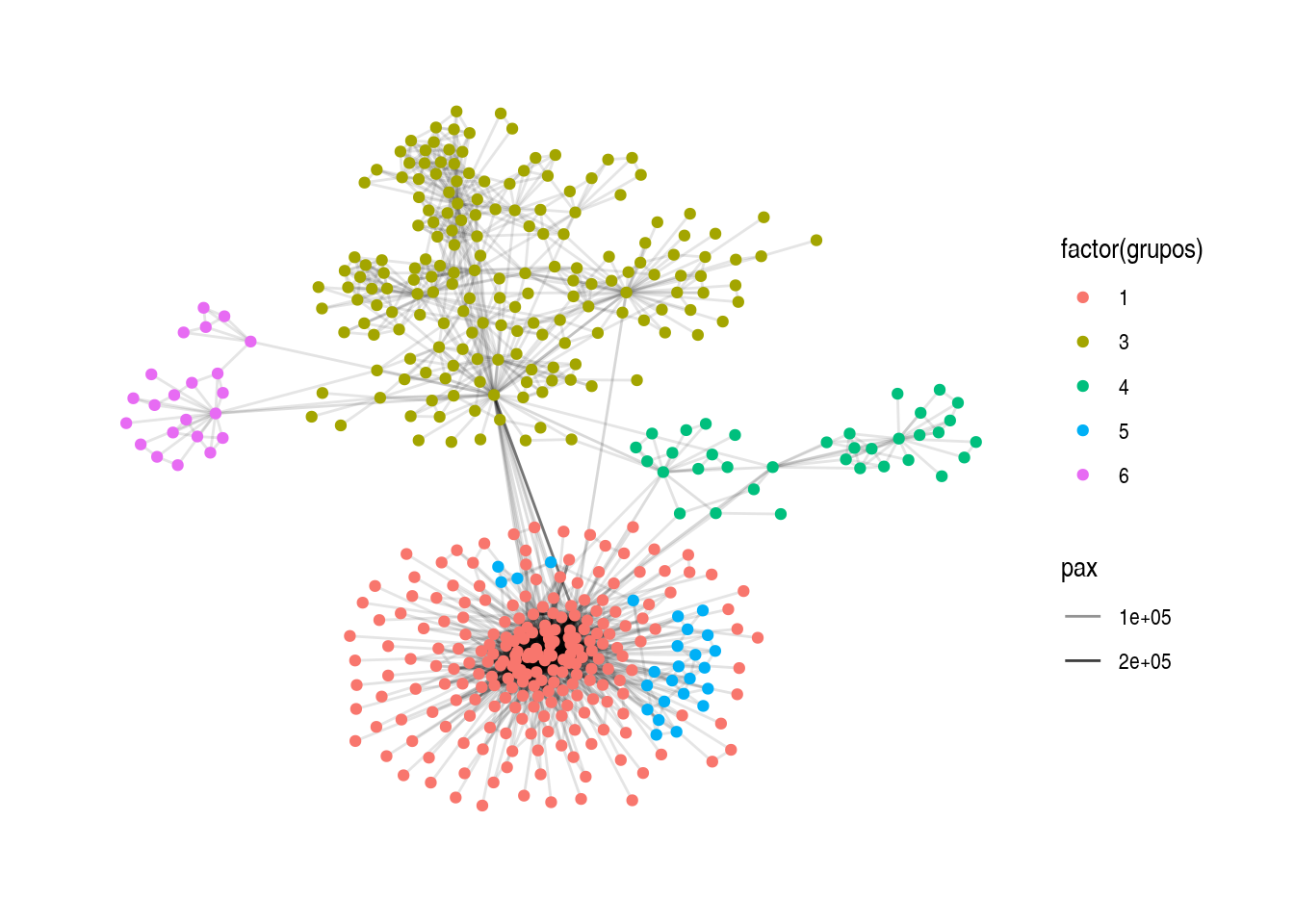
Podemos examinar otras soluciones:
grupos_10 <- igraph::fastgreedy.community(rutas) %>%
igraph::cut_at(10)
rutas <- rutas %>% activate(nodes) %>% mutate(grupos_10 = grupos_10)
igraph::modularity(rutas, as.factor(grupos_10))## [1] 0.4213694ggraph(layout_rutas) +
geom_edge_link(aes(alpha = pax)) +
geom_node_point(aes(colour = factor(grupos_10))) +
theme_graph()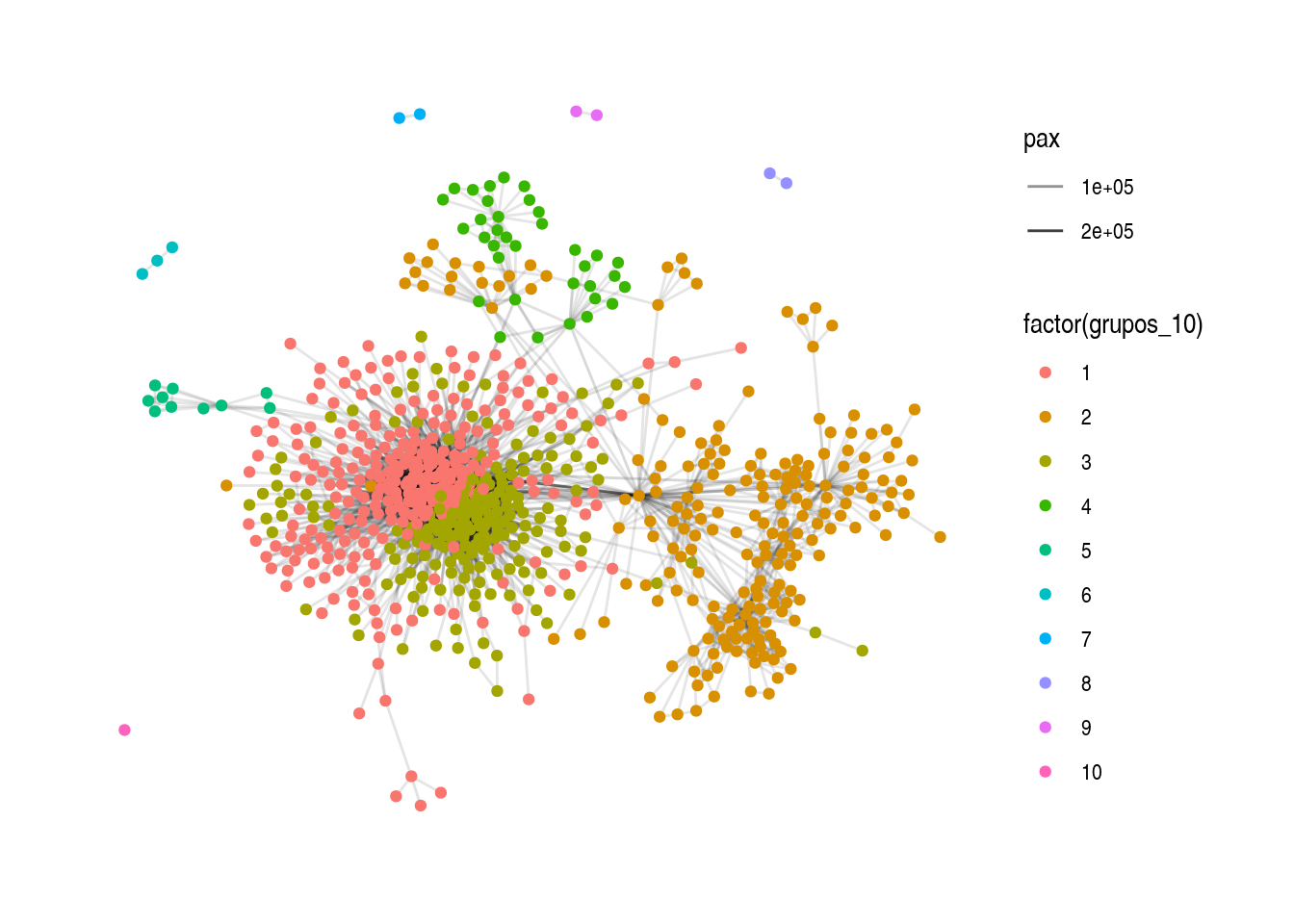
Referencias
Clauset, Aaron, Mark E. J. Newman, and Cristopher Moore. 2004. “Finding Community Structure in Very Large Networks.” Physical Review. E, Statistical, Nonlinear, and Soft Matter Physics 70 6 Pt 2: 066111.
Leskovec, Jure, Anand Rajaraman, and Jeffrey David Ullman. 2014. Mining of Massive Datasets. 2nd ed. New York, NY, USA: Cambridge University Press. http://www.mmds.org.