3 Similitud: Locality sensitive hashing

En la sección anterior vimos como producir una representación de dimensión baja usando funciones hash (firmas minhash), e introdujimos la idea de LSH para poner a los documentos en cubetas, de forma que pares de documentos similares tienen probabilidad alta de caer en la misma cubeta.

En esta sección detallamos este proceso, y también generalizamos para utilizar con otros tipos de medida de similitud.

3.1 Análisis de la técnica de bandas

En la sección anterior dimos la primera idea como usar la técnica de bandas con minhashes para encontrar documentos de similitud alta, con distintos umbrales de similitud alta. Aquí describimos un análisis más detallado de la técnica

Supongamos que tenemos un total de \(k\) minhashes, que dividimos en \(b\) bandas de tamaño \(r\), de modo que \(k=br\).

Decimos que un par de documentos coinciden en una banda de \(r\) hashes si coinciden en todos los hashes de esa banda.
Un par de documentos es un par candidato si al menos coinciden en una banda (es decir, en al menos dentro de una banda todos los minhashes coinciden).

Ahora vamos a calcular la probabilidad de que un par de documentos con similitud \(s\) sean un par candidato:

La probabilidad de que estos dos documentos coincidan en un hash particular es \(s\), la similitud de Jaccard.
La probabiliad de que todos los hashes de una banda coincidan es \(s^r\), pues seleccionamos los hashes independientemente.
Así que la probabilidad de que los documentos no coincidan en una banda particular es: \(1-s^r\)
Esto implica que la probabilidad de que los documentos no coincidan en ninguna banda es \((1-s^r)^b\).
Finalmente, la probabilidad de que estos dos documentos sean un par candidato es \(1-(1-s^r)^b\), que es la probabilidad de que coincidan en al menos una banda.

Si la similitud de Jaccard de dos documentos es \(s\), la probabilidad de que sean un par candidato es igual a \[1-(1-s^r)^b\].

Ejemplo

Supongamos que tenemos \(8\) minhashes, y que nos interesa encontrar documentos con similitud mayor a \(0.7\). Tenemos las siguientes posiblidades:

r <- c(1,2,4,8)
df_br <- tibble(r = r, b = rev(r))
graficar_curvas(df_br) + geom_vline(xintercept = 0.7)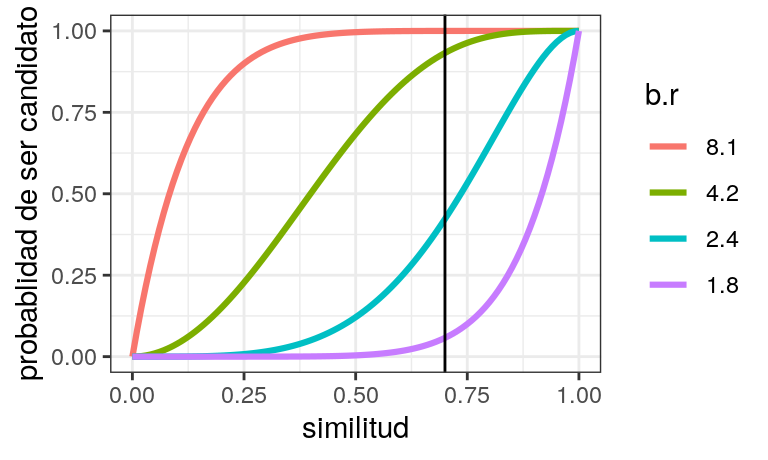

Con la configuración \(b=1, r=8\) (un solo grupo de 8 hashes) es posible que no capturemos muchos pares de la similitud que nos interesa (mayor a \(0.7\)).
Con \(b=8, r=1\) (al menos un hash de los \(8\)), dejamos pasar falsos positivos, que después vamos a tener que filtrar. Esta de cualquier forma puede ser buena estrategia, pues en muchos casos la similitud de la mayoría de los pares es muy cercana a cero.
Los otros dos casos son mejores para nuestro propósito. \(b=4\) produce falsos negativos que hay que filtrar, y para \(b=2\) hay una probabilidad de alrededor de \(50\%\) de que no capturemos pares con similitud cercana a \(0.7.\)

Generalmente quisiéramos obtener algo más cercano a una función escalón. Podemos acercarnos si incrementamos el número total de hashes.

r <- c(4, 5, 8, 10, 20)
b <- 80/r
graficar_curvas(tibble(b, r)) + geom_vline(xintercept = 0.7)

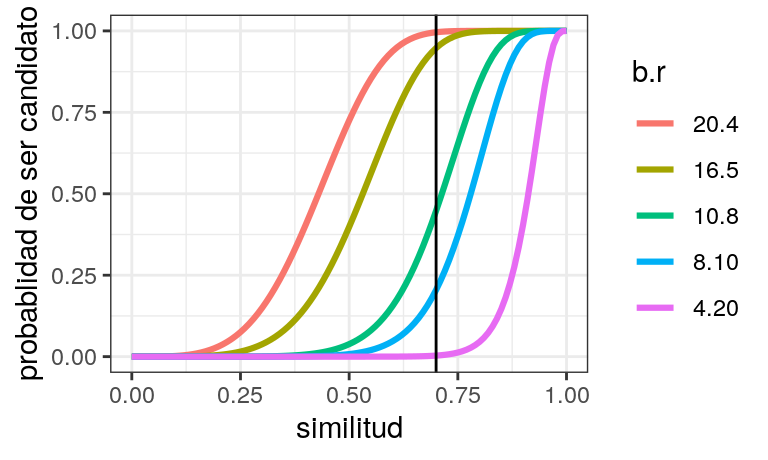
Observación: La curva alcanza probabilidad \(1/2\) cuando la similitud es \[s = \left (1-\left (0.5\right )^{1/b} \right )^{1/r}.\] Y podemos usar esta fórmula para escoger valores de \(b\) y \(r\) apropiados, dependiendo de que similitud nos interesa capturar (quizá moviendo un poco hacia abajo si queremos tener menos falsos negativos).

lsh_half <- function(h, b){
    # h es el número total de funciones hash
   (1 - (0.5) ^ ( 1/b))^(b/h)
}
lsh_half(80, 16)

## [1] 0.5314549

En (Leskovec, Rajaraman, and Ullman 2014), se utiliza la aproximación (según la referencia, aproxima el punto de máxima pendiente):

textreuse::lsh_threshold

## function (h, b) 
## {
##     assert_that(is.count(h), is.count(b), check_banding(h, b))
##     (1/b)^(1/(h/b))
## }
## <bytecode: 0x556a3582cdd8>
## <environment: namespace:textreuse>

Que está también implementada en el paquete textreuse (Mullen 2016).

textreuse::lsh_threshold(80, 16)

## [1] 0.5743492

Ejemplo

Supongamos que nos interesan documentos con similitud mayor a \(0.5\). Intentamos con \(50\) o \(200\) hashes algunas combinaciones:

params_umbral <- function(num_hashes, umbral_inf = 0.0, umbral_sup = 1.0){
  # selecciona combinaciones con umbral-1/2 en un rango 
  # (umbral_inf, umbral_sup)
  b <- seq(1, num_hashes)
  b <- b[num_hashes %% b == 0] # solo exactos
  r <- floor(num_hashes %/% b)
  combinaciones_pr <- 
    tibble(b = b, r = r) %>%
    unique() %>%
    mutate(s = (1 - (0.5)^(1/b))^(1/r)) %>%
    filter(s < umbral_sup, s > umbral_inf)
  combinaciones_pr
}
combinaciones_50 <- params_umbral(50, 0.2, 0.8)
graficar_curvas(combinaciones_50) + 
  geom_vline(xintercept = 0.4, lty=2) + 
   geom_vline(xintercept = 0.7, lty=2)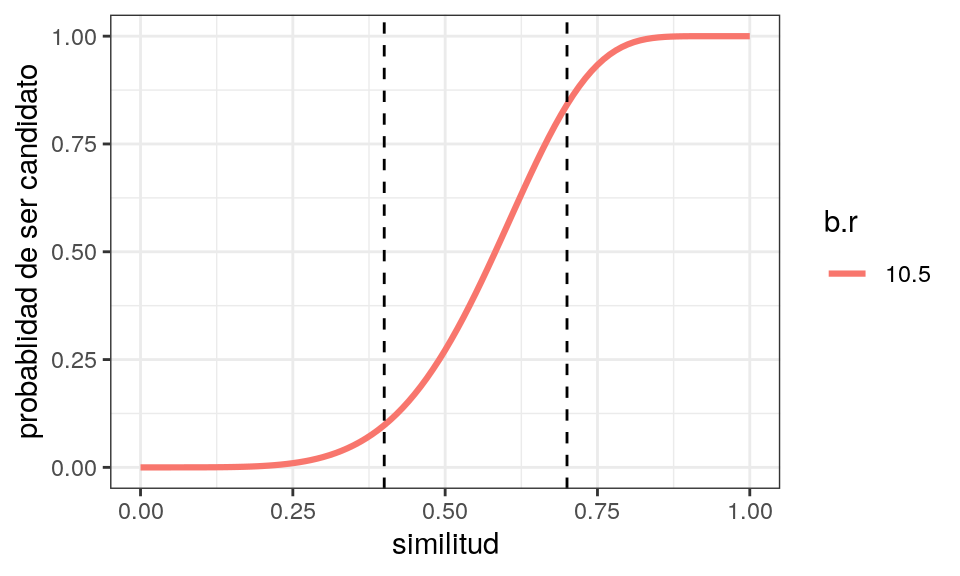

Con \(200\) hashes podemos obtener curvas con mayor pendiente:

combinaciones_200 <- params_umbral(200, 0.2, 0.8)
graficar_curvas(combinaciones_200) + 
  geom_vline(xintercept = 0.2, lty=2) + 
   geom_vline(xintercept = 0.8, lty=2)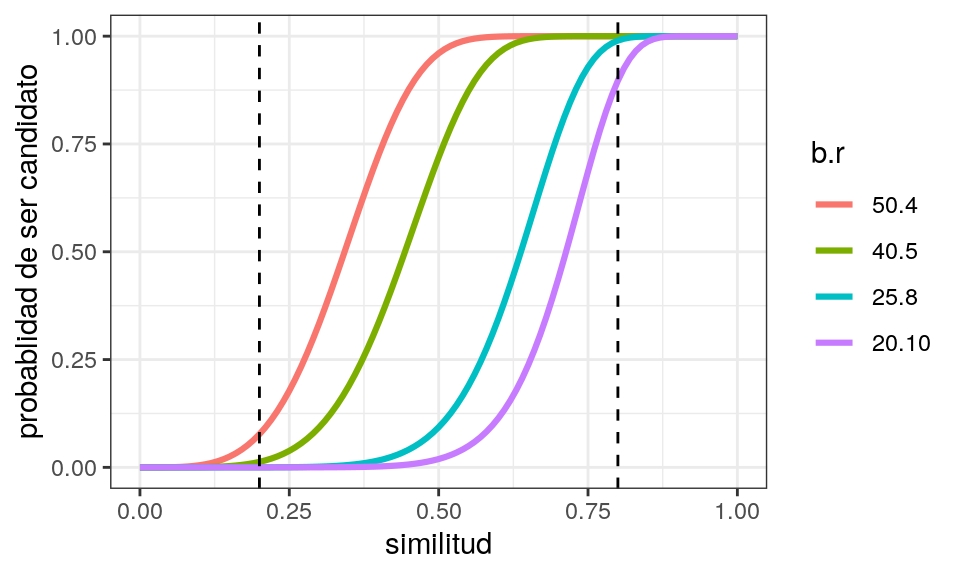

Observación: La decisión de los valores para estos parámetros debe balancear 1. qué tan importante es tener pares no detectados (falsos negativos), y 2. el cómputo necesario para calcular los hashes y filtrar los falsos positivos. La ventaja computacional de LSH proviene de hacer trade-offs de lo que es más importante para nuestro problema.

3.2 Resumen de LSH basado en minhashing

Resumen de (Leskovec, Rajaraman, and Ullman 2014)

Escogemos un número \(k\) de tamaño de tejas, y construimos el conjunto de tejas de cada documento.
Ordenar los pares documento-teja y agrupar por teja.
Escoger \(n\), el número de minhashes. Aplicamos el algoritmo de la clase anterior (teja por teja) para calcular las firmas minhash de todos los documentos.
Escoger el umbral \(s\) de similitud que nos ineresa. Escogemos \(b\) y \(r\) (número de bandas y de qué tamaño), usando la fórmula de arriba hasta obtener un valor cercano al umbral. Si es importante evitar falsos negativos, escoger valores de \(b\) y \(r\) que den un umbral más bajo, si la velocidad es importante entonces escoger para un umbral más alto y evitar falsos positivos. Mayores valores de \(b\) y \(r\) pueden dar mejores resultados, pero también requieren más cómputo.
Construir pares similares usando LSH.
Examinar las firmas de cada par candidato y determinar si la fracción de coincidencias sobre todos los minhashes es satisfactorio. Alternativamente (más preciso), calcular directamente la similitud de Jaccard a partir de las tejas originales.

Alternativamente, podemos:

Agrupar las tejas de cada documento.
Escoger \(n\), el número de minhashes. Calcular el minhash de cada documento aplicando una función hash a las tejas del documento. Tomar el mínimo. Repetir para cada función hash.

3.3 Ejemplo: artículos de wikipedia

En este ejemplo intentamos encontrar artículos similares de wikipedia usando las categorías a las que pertenecen. En lugar de usar tejas, usaremos categorías a las que pertenecen. Dos artículos tienen similitud alta cuando los conjuntos de categorías a las que pertenecen es similar. (este el ejemplo original).

Empezamos con una muestra de los datos:

head -20 ../datos/similitud/wiki-100000.txt

## # 2012-06-04T11:00:11Z
## Autism Autism
## Autism Communication_disorders
## Autism Mental_and_behavioural_disorders
## Autism Neurological_disorders
## Autism Neurological_disorders_in_children
## Autism Pervasive_developmental_disorders
## Autism Psychiatric_diagnosis
## Autism Learning_disabilities
## Anarchism Anarchism
## Anarchism Political_culture
## Anarchism Political_ideologies
## Anarchism Social_theories
## Anarchism Anti-fascism
## Anarchism Greek_loanwords
## Agricultural_science Agronomy
## Albedo Climate_forcing
## Albedo Climatology
## Albedo Electromagnetic_radiation
## Albedo Radiometry

Leemos y limpiamos los datos:

limpiar <- function(lineas,...){
  df_lista <- str_split(lineas, ' ') %>% 
    keep(function(x) x[1] != '#') %>%
    transpose %>%
    map(function(col) as.character(col)) 
  df <- tibble(articulo = df_lista[[1]], 
                   categorias = df_lista[[2]]) 
  df
}
filtrado <- read_lines_chunked('../datos/similitud/wiki-100000.txt',
                    skip = 1, callback = ListCallback$new(limpiar))
articulos_df <- filtrado %>% bind_rows %>%
                group_by(articulo) %>%
                summarise(categorias = list(categorias))
nrow(articulos_df)

## [1] 15976

set.seed(99)
muestra <- articulos_df %>% sample_n(10)
muestra

## # A tibble: 10 x 2
##    articulo                            categorias
##    <chr>                               <list>    
##  1 Gamemaster                          <chr [2]> 
##  2 James_K._Polk                       <chr [27]>
##  3 Psychological_statistics            <chr [4]> 
##  4 Wipe_(transition)                   <chr [3]> 
##  5 Casuistry                           <chr [5]> 
##  6 Telecommunications_in_Guinea-Bissau <chr [1]> 
##  7 Phospholipid                        <chr [1]> 
##  8 Computer_program                    <chr [2]> 
##  9 Information_Sciences_Institute      <chr [5]> 
## 10 Politics_of_Liberia                 <chr [1]>

muestra$categorias[[3]]

## [1] "Psychometrics"                       "Psychology_experiments"             
## [3] "Psychology_lists"                    "Fields_of_application_of_statistics"

Selección de número de hashes y bandas

Ahora supongamos que buscamos artículos con similitud mínima de \(0.4\). Experimentando con valores del total de hashes y el número de bandas, podemos seleccionar, por ejemplo:

b <- 20
num_hashes <- 60
lsh_half(num_hashes, b = b)
## [1] 0.3241633
graficar_curvas(tibble(b = b, r = num_hashes/b)) +
                 geom_vline(xintercept = 0.4)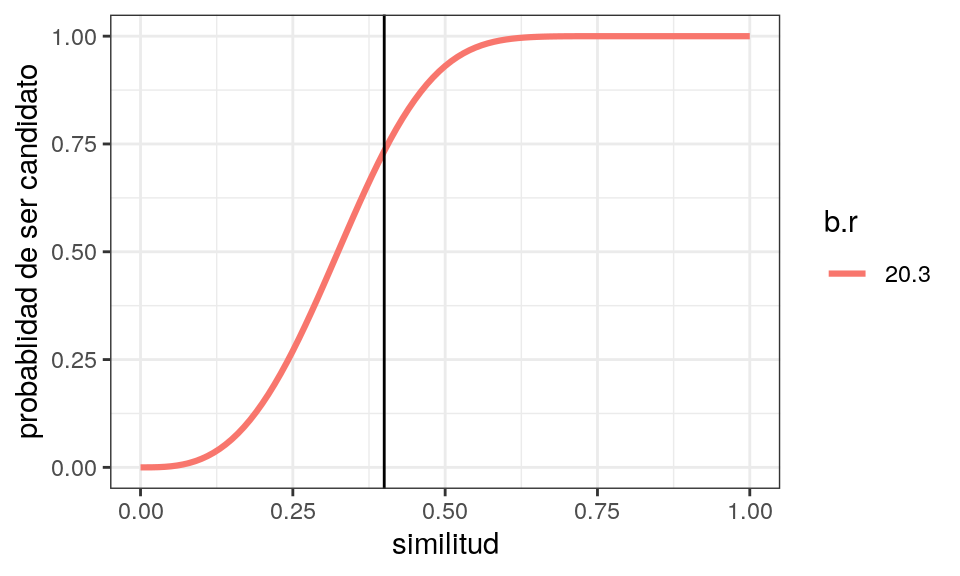

Tejas y cálculo de minhashes

source('../scripts/lsh/minhash.R')

set.seed(28511)
num_hashes <- 60
hash_f <- map(1:num_hashes, ~ generar_hash())
tokenize_sp <- function(x,...) stringr::str_split(x, "[ _]")

# nos podemos ahorrar la siguiente línea si adaptamos crear_tejas_doc
articulos <- articulos_df$articulo
textos <- articulos_df$categorias %>% map_chr( ~ paste(.x, collapse = " ")) 
tejas_obj <- crear_tejas_str(textos, k = 1, tokenize_sp)
firmas_wiki <- calcular_firmas_doc(tejas_obj, hash_f)
head(firmas_wiki)

## # A tibble: 6 x 2
##   doc_id firma     
##    <int> <list>    
## 1      1 <dbl [60]>
## 2      2 <dbl [60]>
## 3      3 <dbl [60]>
## 4      4 <dbl [60]>
## 5      5 <dbl [60]>
## 6      6 <dbl [60]>

Agrupación en cubetas

Ahora calculamos las cubetas y agrupamos:

particion <- split(1:60,  ceiling(1:60 / 3))
sep_cubetas <- separar_cubetas_fun(particion)
sep_cubetas(firmas_wiki$firma[[1]])

##                                            1 
##         "123|-66172933/950495008/-646756207" 
##                                            2 
##    "456|-1763260935/-1205811513/-1905189324" 
##                                            3 
##       "789|-1061946219/102680258/-782320690" 
##                                            4 
##   "101112|-420190316/-652837401/-2115263585" 
##                                            5 
##     "131415|-86857139/576249311/-1664081995" 
##                                            6 
##    "161718|-32174279/-767628714/-1767723808" 
##                                            7 
##     "192021|-1975143711/552804685/227027734" 
##                                            8 
##   "222324|-884718086/1082289999/-2033877798" 
##                                            9 
##  "252627|-2033709367/-921276105/-1995352702" 
##                                           10 
##  "282930|-1180592712/-319871159/-1351016162" 
##                                           11 
##  "313233|-1014299443/-1025095826/-865016319" 
##                                           12 
##     "343536|444868994/-1438093550/308849441" 
##                                           13 
## "373839|-1385735001/-1741005613/-1642346961" 
##                                           14 
##    "404142|-2005881243/1239002253/515209681" 
##                                           15 
## "434445|-1954345753/-1895973888/-2125568934" 
##                                           16 
##  "464748|-284721374/-1741352340/-1731737688" 
##                                           17 
##     "495051|140991328/-603256911/1280707567" 
##                                           18 
##      "525354|435112914/1421133606/625421078" 
##                                           19 
##  "555657|-1623633559/-2114113684/-189162434" 
##                                           20 
##      "585960|-710910843/-421725193/14236182"

lsh_wiki <- firmas_wiki %>% 
    mutate(cubeta = map(firma, sep_cubetas)) %>% 
    select(-firma) %>% unnest_legacy %>% 
    group_by(cubeta) %>% 
    summarise(docs = list(doc_id), n = length(doc_id)) %>% 
    mutate(n_docs = map(docs, length))
lsh_wiki

## # A tibble: 253,274 x 4
##    cubeta                                     docs          n n_docs   
##    <chr>                                      <list>    <int> <list>   
##  1 101112|-1000844464/-1148934697/-1655495427 <int [1]>     1 <int [1]>
##  2 101112|-1001213340/-845483284/-1158801321  <int [1]>     1 <int [1]>
##  3 101112|-1001213340/-845483284/-1685970544  <int [1]>     1 <int [1]>
##  4 101112|-1001853179/-1436608097/-1154683234 <int [3]>     3 <int [1]>
##  5 101112|-1001853179/-1436608097/-1213525930 <int [1]>     1 <int [1]>
##  6 101112|-1001853179/-1436608097/-1913362101 <int [1]>     1 <int [1]>
##  7 101112|-1002453998/-1802803867/-1722980031 <int [1]>     1 <int [1]>
##  8 101112|-1003660910/511232892/296557711     <int [1]>     1 <int [1]>
##  9 101112|-1006781051/-1060609409/-2025078977 <int [1]>     1 <int [1]>
## 10 101112|-1007119622/472051802/-1054303145   <int [1]>     1 <int [1]>
## # … with 253,264 more rows

Filtramos las cubetas que tienen más de un documento:

lsh_agrupados <- lsh_wiki %>%  
    filter(n_docs > 1)

Y ahora examinamos algunos de las cubetas que encontramos de artículos similares según sus categorías:

imprimir_texto <- function(indices){
    for(ind in indices){
        print(paste(articulos[ind]))
        print(paste("      ", textos[ind]))
    }
}
imprimir_texto(lsh_agrupados$docs[[39]])

## [1] "Declarative_memory"
## [1] "       Memory_processes"
## [1] "Forgetting"
## [1] "       Memory_processes"
## [1] "Forgetting_curve"
## [1] "       Memory_processes"
## [1] "Long-term_memory"
## [1] "       Memory_processes"
## [1] "Short-term_memory"
## [1] "       Memory_processes"

imprimir_texto(lsh_agrupados$docs[[2615]])

## [1] "Chemical_affinity"
## [1] "       Physical_chemistry"
## [1] "Chemical_thermodynamics"
## [1] "       Thermodynamics Chemical_thermodynamics Physical_chemistry Branches_of_thermodynamics"
## [1] "Electrochemistry"
## [1] "       Electrochemistry Physical_chemistry"
## [1] "Fick's_laws_of_diffusion"
## [1] "       Diffusion Statistical_mechanics Physical_chemistry Mathematics_in_medicine"
## [1] "Law_of_dilution"
## [1] "       Physical_chemistry Enzyme_kinetics"
## [1] "Law_of_multiple_proportions"
## [1] "       Physical_chemistry"
## [1] "Physical_chemistry"
## [1] "       Physical_chemistry"
## [1] "Thermochemistry"
## [1] "       Physical_chemistry Thermochemistry Branches_of_thermodynamics"

imprimir_texto(lsh_agrupados$docs[[11521]])

## [1] "German_Type_II_submarine"
## [1] "       Type_II_U-boats Submarine_classes World_War_II_submarines_of_Germany"
## [1] "German_Type_IX_submarine"
## [1] "       Type_IX_U-boats Submarine_classes World_War_II_submarines_of_Germany"
## [1] "German_Type_VII_submarine"
## [1] "       Type_VII_U-boats Submarine_classes World_War_II_submarines_of_Germany"

imprimir_texto(lsh_agrupados$docs[[255]])

## [1] "Economy_of_Chile"
## [1] "       Economy_of_Chile Organisation_for_Economic_Co-operation_and_Development_member_economies World_Trade_Organization_member_economies"
## [1] "Economy_of_Israel"
## [1] "       Economy_of_Israel Organisation_for_Economic_Co-operation_and_Development_member_economies World_Trade_Organization_member_economies"
## [1] "Economy_of_Mexico"
## [1] "       Economy_of_Mexico Organisation_for_Economic_Co-operation_and_Development_member_economies World_Trade_Organization_member_economies"
## [1] "Economy_of_New_Zealand"
## [1] "       Economy_of_New_Zealand World_Trade_Organization_member_economies Organisation_for_Economic_Co-operation_and_Development_member_economies"
## [1] "Economy_of_Turkey"
## [1] "       World_Trade_Organization_member_economies Organisation_for_Economic_Co-operation_and_Development_member_economies Economy_of_Turkey"

Ejercicio: explora más los grupos creados por las cubetas. Observa que pares similares dados pueden ocurrir en más de una cubeta (pares repetidos)

Creación de pares candidatos y falsos positivos

Creamos ahora todos los posibles pares candidatos: obtenemos pares de las cubetas y calculamos pares únicos:

candidatos <- extraer_pares(lsh_agrupados, cubeta, docs, textos) 
candidatos

## # A tibble: 385,467 x 4
##        a     b texto_a                          texto_b                         
##    <int> <int> <chr>                            <chr>                           
##  1  2405  7096 Differentiation_rules Articles_… Calculus History_of_mathematics…
##  2  2405  8183 Differentiation_rules Articles_… Lambda_calculus Fictional_knigh…
##  3  7096  8183 Calculus History_of_mathematics… Lambda_calculus Fictional_knigh…
##  4  3219 13244 Card_game_terminology            Card_game_terminology Randomnes…
##  5  5818  6734 Geography_of_Tonga               History_of_Tonga                
##  6  5777  6689 Geography_of_Sierra_Leone        History_of_Sierra_Leone         
##  7  5777 11546 Geography_of_Sierra_Leone        Politics_of_Sierra_Leone        
##  8  5777 12427 Geography_of_Sierra_Leone        Military_of_Sierra_Leone        
##  9  5777 14260 Geography_of_Sierra_Leone        Communications_in_Sierra_Leone  
## 10  5777 14974 Geography_of_Sierra_Leone        Transport_in_Sierra_Leone       
## # … with 385,457 more rows

Y nos queda por evaluar estos pares para encontrar la similitud exacta y poder descartar falsos positivos:

candidatos <- candidatos %>% 
  mutate(sim = map2_dbl(texto_a, texto_b, function(ta, tb){
            sim_jaccard(tokenize_sp(ta)[[1]], tokenize_sp(tb)[[1]])
        }))                                        
nrow(candidatos)

## [1] 385467

cand_filtrados <- candidatos %>% filter(sim > 0.4)
nrow(cand_filtrados)

## [1] 115582

quantile(cand_filtrados$sim)

##        0%       25%       50%       75%      100% 
## 0.4022989 0.5000000 0.6666667 0.6666667 1.0000000

DT::datatable(cand_filtrados %>% sample_n(2000))

Nótese que este número de comparaciones es órdenes de magnitud más chico del total de posibles comparaciones del corpus completo.

3.4 Medidas de distancia

La técnica de LSH puede aplicarse a otras medidas de distancia, con otras formas de hacer hash diferente del minhash. La definición de distancia puedes consultarla aquí

Distancia de Jaccard

Puede definirse simplemente como \[1-sim(a,b),\] donde \(a\) y \(b\) son conjuntos y \(sim\) es la similitud de Jaccard.

Distancia euclideana

Es la distancia más común para vectores de números reales:

Si \(x=(x_1,\ldots, x_p)\) y \(y=(y_1,\ldots, y_p)\) son dos vectores, su norma \(L_2\) está dada por

\[ d(x,y) = \sqrt{\sum_{i=1}^p (x_i-y_i)^2 } = ||x-y||\]

Distancia coseno

La distancia coseno, definida también para vectores de números reales, no toma en cuenta la magnitud de vectores, sino solamente su dirección.

La similitud coseno se define primero como \[sim_{cos}(x,y) = \frac{<x, y>}{||x||||y||} = \cos (\theta)\] donde \(<x, y> = \sum_{i=1}^p x_iy_i\) es el producto punto de \(x\) y \(y\). Esta cantidad es igual al coseno del ángulo entre los vectores \(x\) y \(y\) (¿por qué?).

La distancia coseno es entones \[d_{cos}(x,y) = 1- sim_{cos}(x,y).\]

Esta distancia es útil cuando el tamaño general de los vectores no nos importa. Como veremos más adelante, una aplicación usual es comparar documentos según las frecuencias de los términos que contienen: en este caso, nos importa más la frecuencia relativa de los términos que su frecuencia absoluta (pues esta última también refleja la el tamaño de los documentos).

A veces se utiliza la distancia angular (medida con un número entre 0 y 180), que se obtiene de la distancia coseno, es decir, \[d_a(x,y) = \theta,\] donde \(\theta\) es tal que \(\cos(\theta) = d_{cos}(x,y).\)

3.4.1 Distancia de edición

Esta es una medida útil para medir distancia entre cadenas. La distancia de edición entre dos cadenas \(x=x_1\cdots x_n\) y \(y=y_1\cdots y_n\) es el número mínimo de inserciones y eliminaciones (un caracter a la vez) para convertir a \(x\) en \(y\).

Por ejemplo, la distancia entre “abcde” y “cefgh” se calcula como sigue: para pasar de la primera cadena, necesitamos agregar \(f\), \(g\) y \(h\) (\(3\) adiciones), eliminar \(d\), y eliminar \(a,b\) (\(3\) eliminaciones). La distancia entre estas dos cadenas es \(6\).

3.5 Teoría de funciones sensibles a la localidad

Vimos como la familia de funciones minhash puede combinarse (usando la técnica de bandas) para discriminar entre pares de baja similitud y de alta similitud.

En esta parte consideramos otras posibles familias de funciones para lograr lo mismo bajo otras medidas de distancia. Veamos las características básicas de las funciones \(f\) del minhash:

Cuando la distancia entre dos elementos \(x,y\) es baja (similitud alta), entonces una colisión \(f(x)=f(y)\) tiene probabilidad alta.
Podemos escoger al azar entre varias funciones \(f_1,\ldots,f_k\) con la propiedad anterior, de manera independiente, de forma que es posible calcular (o acotar) la probabilidad de \(f_i(x)=f_i(y)\) .
Las funciones tienen que ser relativamente fáciles de calcular (comparado con calcular todos los posibles pares y sus distancias directamente).

3.6 Funciones sensibles a la localidad

Sean \(d_1<d_2\) dos valores (que interpretamos como distancias). Una familia \({\cal F}\) es una familia \(d_1,d_2,p_1,p_2\), sensible a localidad (con \(p_1>p_2\)) cuando para cualquier par de elementos \(x,y\),

Si \(d(x,y)\leq d_1\), entonces la probabilidad \(P(f(x)=f(y))\geq p_1\).
Si \(d(x,y)\geq d_2\), entonces \(P(f(x)=f(y))\leq p_2\)

Nótese que las probabilidades están dadas sobre la selección de \(f\).

Estas condiciones se interpretan como sigue: cuando \(x\) y \(y\) están suficientemente cerca (\(d_1\)), la probabilidad de que sean mapeados al mismo valor por una función \(f\) de la familia es alta. Cuando \(x\) y \(y\) están lejos \(d_2\), entonces, la probabilidad de que sean mapeados al mismo valor es baja. Podemos ver una gráfica:

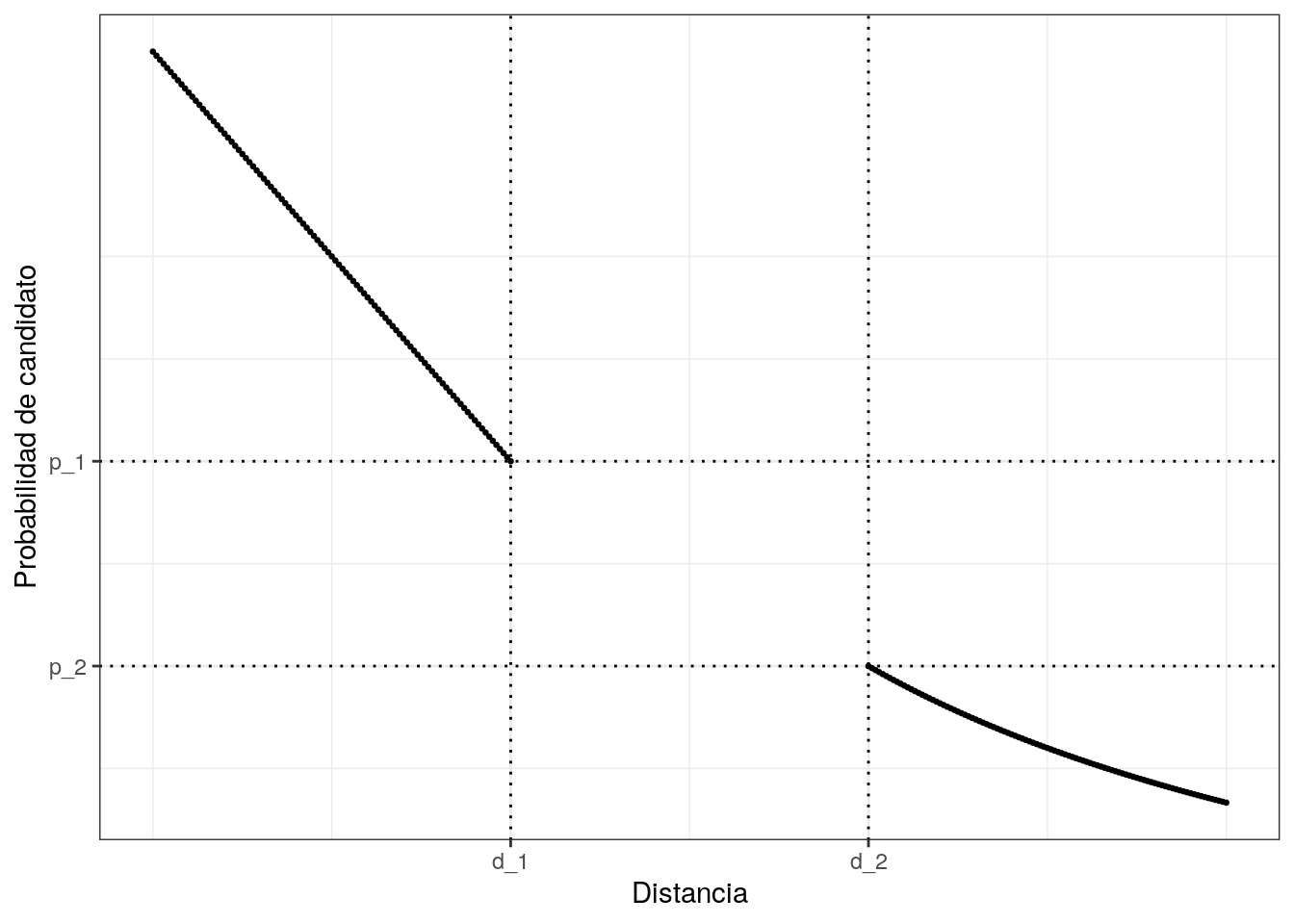
3.6.1 Distancia Jaccard

Supongamos que tenemos dos documentos \(x,y\). Si ponemos por ejemplo \(d_1=0.2\) y \(d_2= 0.5\), tenemos que si \(d(x,y) = 1-sim(x,y) \leq 0.2\), despejando tenemos \(sim(x,y)\geq 0.8\), y entonces \[P(f(x) = f(y)) = sim(x,y) \geq 0.8\] Igualmente, si \(d(x,y)=1-sim(x,y) \geq 0.5\), entonces \[P(f(x) = f(y)) = sim(x,y) \leq 0.5\] de modo que la familia de minhashes es \((0.2,0.5,0.8,0.5)\) sensible a la localidad

Para cualquier \(d_1 < d_2\), la familia de funciones minhash es una familia \((d_1, d_2, 1-d_1, 1-d_2)\) sensible a la localidad para cualquier \(d_1\leq d_2\).

3.7 Amplificación de familias sensibles a la localidad

Con una familia sensible a la localidad es posible usar la técnica de bandas para obtener la discriminación de similitud que nos interese.

Supongamos que \({\cal F}\) es una familia \((d_1, d_2, p_1, p_2)\)-sensible a la localidad. Podemos usar conjunción de \({\cal F}'\) para construir otra familia sensible a la localidad.

Sea \(r\) un número entero. Una función \(f\in {\cal F}'\) se construye tomando \(f = (f_1,f_2,\ldots, f_r)\), con \(f_i\) seleccionadas al azar de manera independiente de la familia original, de forma que \(f(x)=f(y)\) si y sólo si \(f_i(x)=f_i(y)\) para toda \(i\). Esta construcción corresponde a lo que sucede dentro de una banda de la técnica de LSH.

La nueva familia \({\cal F}'\) es \((d_1,d_2,p_1^r,p_2^r)\) sensible a la localidad. Nótese que las probabilidades siempre se hacen más chicas cuando incrementamos \(r\), lo que hace más fácil eliminar pares con similitudes en niveles bajos.

Podemos también hacer disyunción de una familia \({\cal F}\). En este caso, decimos que \(f(x)=f(y)\) cuando al menos algún \(f_i(x)=f_i(y)\).

En este caso, la disyunción da una familia \((d_1,d_2,1-(1-p_1)^b,1-(1-p_2)^b)\) sensible a la localidad. Esta construcción es equivalente a construir varias bandas.

La idea general es ahora:

Usando conjunción, podemos construir una familia donde la probabilidad \(p_2^r\) sea mucho más cercana a cero que \(p_1^r\) (en términos relativos).
Usando disyunción, podemos construir una familia donde la probabilidad \(1-(1-p_1^r)^b\) permanece cercana a \(1\), pero \(1-(1-p_2^r)^b\) está cerca de cero.
Combinando estas operaciones usando la técnica de bandas podemos construir una famlia que discrimine de manera distinta entre distancias menores a \(d_1\) y distancias mayores a \(d_2\).
El costo incurrido es que tenemos que calcular más funciones para discriminar mejor.

Ejercicio

Supongamos que tenemos una familia \((0.2, 0.6, 0.8, 0.4)\) sensible a la localidad. Si combinamos con conjunción 4 de estas funciones, obtenemos una familia \[(0.2, 0.6, 0.41, 0.026)\] La proporción de falsos positivos es chica, pero la de falsos negativos es grande. Si tomamos 8 de estas funciones (cada una compuesta de cuatro funciones de la familia original) y hacemos conjunción, obtenemos una familia

\[(0.2, 0.6, 0.98, 0.19)\]

En esta nueva familia, tenemos que hacer \(32\) veces más trabajo para tener esta amplificación.

3.8 Distancia coseno e hiperplanos aleatorios

Construimos ahora LSH para datos numéricos, y comenzaremos con la distancia coseno. Lo primero que necesitamos es una familia sensible a la localidad para la distancia coseno.

Consideremos dos vectores, y supongamos que el ángulo entre ellos es chico. Si escogemos un hiperplano al azar, lo más probable es que queden del mismo lado del hiperplano. En el caso extremo, si los vectores apuntan exactamente en la misma dirección, entonces la probabilidad es \(1\).

Sin embargo, si el ángulo entre estos vectores es grande, entonces lo más probable es que queden separados por un hiperplano escogido al azar. Si los vectores son ortogonales (máxima distancia coseno posible), entonces esta probabilidad es \(0\).

Esto sugiere construir una familia sensible a la localidad para la distancia coseno de la siguiente forma:

Tomamos un vector al azar \(v\).
Nos fijamos en la componente de la proyección de \(x\) sobre \(v\)
Ponemos \(f_v(x)=1\) si esta componente es positiva, y \(f_v(x)=-1\) si esta componente es negativa.
Podemos poner simplemente: \[ f_v(x) = signo (<x, v>)\]

Recordatorio: La componente de la proyección de \(x\) sobre \(v\) está dada por el producto interior de \(x\) y \(v\) normalizado: \[\frac{1}{||v||}<x, v>,\] y su signo es el mismo de \(<x,v>\).

La familia descrita arriba (hiperplanos aleatorios) es \((d_1,d_2, (180-d_1)/180, d_2/180)\) sensible a la localidad para la distancia angular.

Vamos a dar un argumento del cálculo: supongamos que el ángulo entre \(x\) y \(y\) es \(d=\theta\), es decir, la distancia angular entre \(x\) y \(y\) es \(\theta\).

Consideramos el plano \(P\) que pasa por el origen y por \(x\) y \(y\). Si escogemos un vector al azar (cualquier dirección igualmente probable), el vector produce un hiperplano perpendicular (son los puntos \(z\) tales que \(<z,v>=0\)) que corta al plano \(P\) en dos partes. Todas las direcciones de corte son igualmente probables, así que la probabilidad de que la dirección de corte separe a \(x\) y \(y\) es igual a \(2\theta /360\) (que caiga en el cono generado por \(x\) y \(y\)). Si la dirección de corte separa a \(x\) y \(y\), entonces sus valores \(f_v(x)\) y \(f_v(y)\) no coinciden, y coinciden si la dirección no separa a \(x\) y \(y\). Así que:

\(d(x,y)=d_1=\theta\), entonces \(P(f(x)=f(y)) = 1-d_1/180.\)

Por otro lado,

\(d(x,y)=d_2\), entonces \(P(f(x)\neq f(y)) = d_2/180.\)

Ejemplo: similitud coseno por fuerza bruta

Comenzamos con un ejemplo simulado.

set.seed(101)
mat_1 <- matrix(rnorm(600 * 2000) + 3, ncol = 2000)
mat_2 <- matrix(rnorm(1200 * 2000) + 0.2, ncol = 2000)
datos_tbl_vars <- rbind(mat_1, mat_2)  %>%
  data.frame %>% 
  add_column(id_1 = 1:1800, .before = 1)
head(datos_tbl_vars[,1:5])

##   id_1       X1        X2       X3       X4
## 1    1 2.673964 2.6106873 4.173149 1.775517
## 2    2 3.552462 1.9273515 2.487071 3.546486
## 3    3 2.325056 2.6046536 2.999862 2.126006
## 4    4 3.214359 2.1550124 2.360873 2.970787
## 5    5 3.310769 2.3440595 3.178497 2.443552
## 6    6 4.173966 0.4930086 3.497458 3.333134

Tenemos entonces \(2000\) variables distintas y \(1800\) casos, y nos interesa filtrar aquellos pares de similitud alta.

Definimos nuestra función de distancia

norma <- function(x){
  sqrt(sum(x ^ 2))
}
dist_coseno <- function(x, y){
  1 - sum(x*y) / (norma(x) * norma(y))
}

Y calculamos todas las posibles distancias (normalmente no queremos hacer esto, pero lo hacemos aquí para comparar):

datos_tbl <- datos_tbl_vars %>%
  pivot_longer(-id_1, names_to = "variable", values_to = "valor") %>% 
  group_by(id_1) %>%
  arrange(variable) %>%
  summarise(vec_1 = list(valor))
system.time(
pares_tbl <- datos_tbl %>% 
    crossing(datos_tbl %>% 
        rename(id_2 = id_1, vec_2 = vec_1)) %>%
    filter(id_1 < id_2) %>%
    mutate(dist = map2_dbl(vec_1, vec_2, dist_coseno))
)

##    user  system elapsed 
##  31.037   0.024  31.062

pares_tbl %>% head

## # A tibble: 6 x 5
##    id_1 vec_1          id_2 vec_2           dist
##   <int> <list>        <int> <list>         <dbl>
## 1     1 <dbl [2,000]>     2 <dbl [2,000]> 0.101 
## 2     1 <dbl [2,000]>     3 <dbl [2,000]> 0.102 
## 3     1 <dbl [2,000]>     4 <dbl [2,000]> 0.102 
## 4     1 <dbl [2,000]>     5 <dbl [2,000]> 0.100 
## 5     1 <dbl [2,000]>     6 <dbl [2,000]> 0.0985
## 6     1 <dbl [2,000]>     7 <dbl [2,000]> 0.101

La distribución de distancias sobre todos los pares es la siguiente: (¿por qué observamos este patrón? Recuerda que esta gráfica representa pares:

qplot(pares_tbl$dist, binwidth = 0.01)

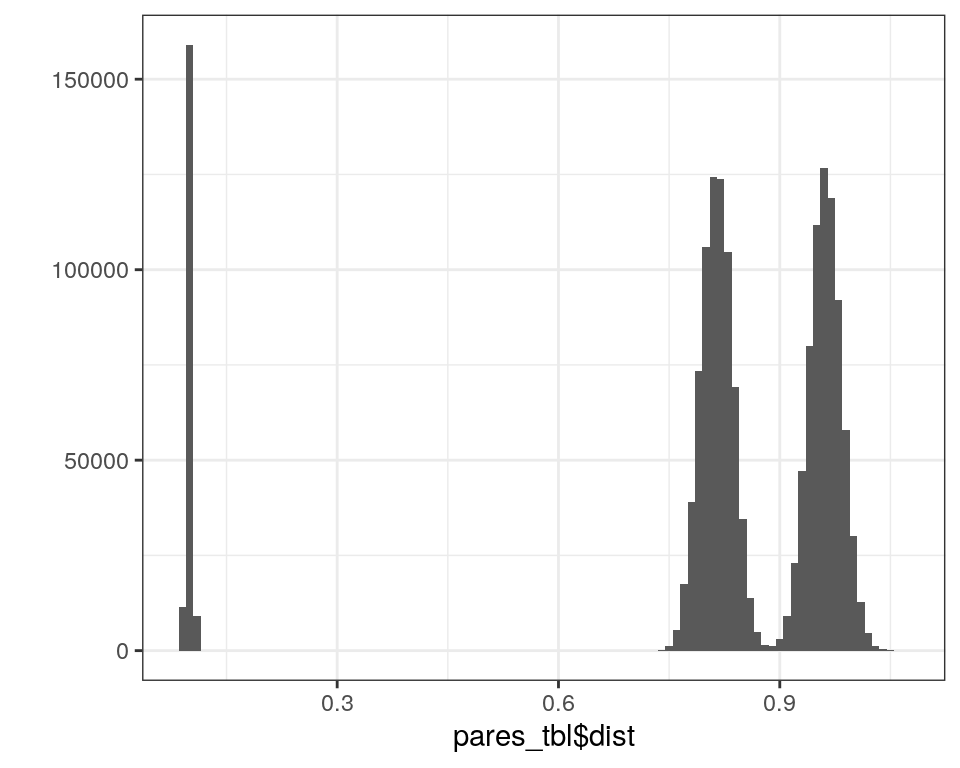
Y supongamos que queremos encontrar vectores con distancia coseno menor a \(0.15\) (menos de unos \(30\) grados). El número de pares que satisfacen esta condicion son:

sum(pares_tbl$dist < 0.15)

## [1] 179700

Ejemplo: LSH planos aleatorios

Usamos \(300\) funciones hash:

crear_hash_sketch <- function(dim) {
  v <- rnorm(dim)
    function(x){
        ifelse(sum(v*x) >= 0, 1L, -1L) 
    }
}
set.seed(101021)
hash_f <- map(1:300, ~ crear_hash_sketch(dim = 2000))

Por ejemplo, la firma del primer elemento es:

z <- datos_tbl$vec_1[[1]]
map_int(hash_f, ~ .x(z))

##   [1]  1  1  1 -1 -1 -1  1  1 -1  1  1  1  1 -1 -1 -1  1  1  1 -1  1 -1  1  1  1
##  [26] -1 -1 -1  1 -1 -1  1 -1  1 -1  1 -1  1 -1  1 -1 -1 -1  1  1 -1 -1  1 -1  1
##  [51]  1  1 -1  1  1  1 -1  1 -1 -1 -1  1  1 -1 -1 -1 -1 -1  1 -1  1  1  1 -1  1
##  [76]  1  1 -1  1 -1 -1 -1 -1 -1 -1  1  1 -1  1 -1  1  1 -1 -1 -1  1  1 -1 -1 -1
## [101]  1  1  1  1 -1  1 -1 -1  1 -1 -1 -1 -1 -1 -1  1  1  1  1  1  1  1 -1  1 -1
## [126]  1  1 -1  1 -1 -1  1  1 -1 -1 -1  1 -1 -1 -1  1  1  1  1  1 -1 -1  1  1  1
## [151] -1  1 -1 -1 -1 -1  1  1  1  1 -1  1 -1 -1  1 -1  1 -1 -1  1 -1 -1 -1  1  1
## [176] -1  1 -1 -1 -1  1 -1 -1 -1 -1  1  1 -1  1 -1 -1 -1  1 -1 -1 -1 -1  1  1  1
## [201]  1  1 -1  1  1  1 -1  1  1  1  1  1 -1  1 -1 -1  1  1 -1 -1  1 -1 -1 -1  1
## [226] -1 -1  1  1 -1  1 -1  1 -1 -1 -1 -1  1  1  1  1  1 -1  1 -1  1 -1  1 -1  1
## [251]  1  1 -1  1 -1  1 -1  1 -1  1  1  1 -1  1  1 -1 -1 -1 -1 -1 -1 -1  1  1 -1
## [276]  1  1 -1 -1  1 -1 -1 -1 -1  1 -1  1  1  1 -1  1  1 -1  1  1 -1  1 -1 -1 -1

Y ahora calculamos la firma para cada elemento:

calculador_hashes <- function(hash_f){
  function(z) {
    map_int(hash_f, ~ .x(z))
  }
}
calc_hashes <- calculador_hashes(hash_f)
hash_tbl <- datos_tbl %>%
  mutate(firma = map(vec_1, ~ calc_hashes(.x))) %>% 
  select(id_1, firma)
hash_tbl

## # A tibble: 1,800 x 2
##     id_1 firma      
##    <int> <list>     
##  1     1 <int [300]>
##  2     2 <int [300]>
##  3     3 <int [300]>
##  4     4 <int [300]>
##  5     5 <int [300]>
##  6     6 <int [300]>
##  7     7 <int [300]>
##  8     8 <int [300]>
##  9     9 <int [300]>
## 10    10 <int [300]>
## # … with 1,790 more rows

Vamos a amplificar la familia de hashes. En este caso, escogemos \(30\) bandas de \(10\) hashes cada una.

b <- 30
r <- 10
f_1 <- function(x){
    1-(1-((180-x)/180)^r)^b
}
curve(f_1, 0, 180)
abline(v=30)

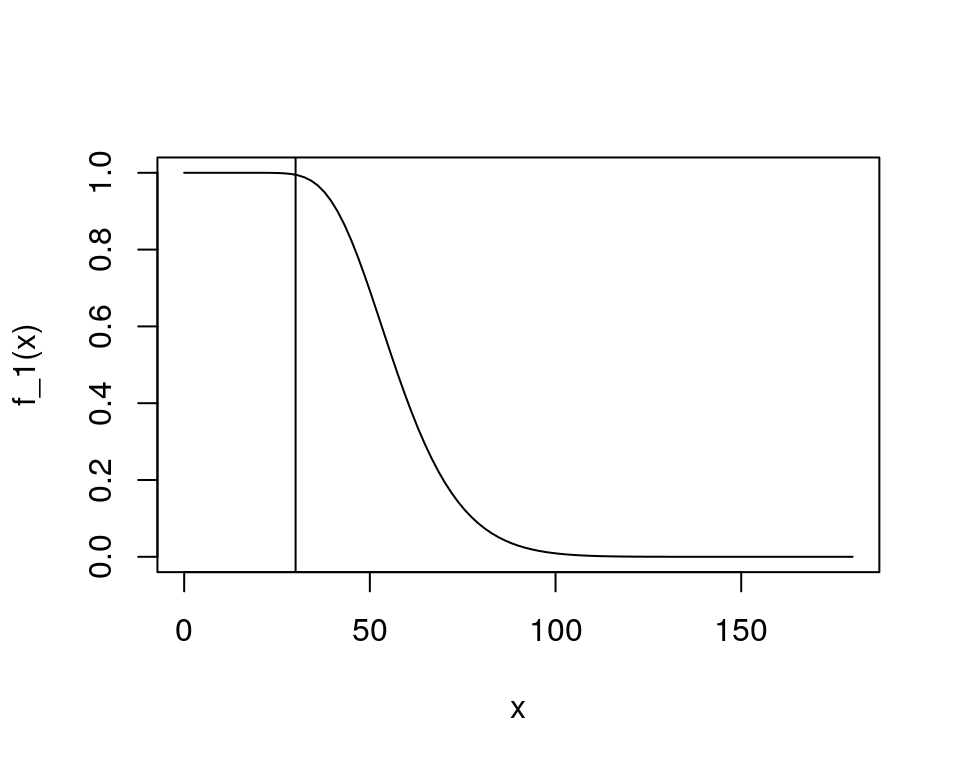
Ejemplo: agrupar por cubetas para LSH

Construimos las cubetas, igual como hacemos en minhashing

particion <- split(1:300, ceiling(1:300 / r))
separar_cubetas_fun <- function(particion){
    function(firma){
        map_chr(particion, function(x){
            prefijo <- paste0(x, collapse = '')
            cubeta <- paste(firma[x], collapse = "/")
            paste(c(prefijo, cubeta), collapse = '|')
        })
    }
}
sep_cubetas <- separar_cubetas_fun(particion)
cubetas_tbl <- hash_tbl %>%
  mutate(cubeta = map(firma, sep_cubetas)) %>% 
  select(-firma) %>% 
  unnest_legacy %>% 
  group_by(cubeta) %>% 
  summarise(ids = list(id_1), n = length(id_1)) %>% 
  arrange(desc(n))

Filtramos las cubetas con más de un caso

cubetas_tbl <- cubetas_tbl %>% filter(n > 1)
cubetas_tbl

## # A tibble: 9,916 x 3
##    cubeta                                                   ids             n
##    <chr>                                                    <list>      <int>
##  1 121122123124125126127128129130|1/1/-1/1/-1/1/1/-1/1/-1   <int [454]>   454
##  2 141142143144145146147148149150|1/1/1/1/1/-1/-1/1/1/1     <int [447]>   447
##  3 211212213214215216217218219220|1/1/-1/1/-1/-1/1/1/-1/-1  <int [408]>   408
##  4 291292293294295296297298299300|1/1/-1/1/1/-1/1/-1/-1/-1  <int [404]>   404
##  5 41424344454647484950|-1/-1/-1/1/1/-1/-1/1/-1/1           <int [393]>   393
##  6 151152153154155156157158159160|-1/1/-1/-1/-1/-1/1/1/1/1  <int [263]>   263
##  7 261262263264265266267268269270|1/1/-1/1/1/-1/-1/-1/-1/-1 <int [263]>   263
##  8 131132133134135136137138139140|-1/1/1/1/-1/-1/1/-1/-1/-1 <int [260]>   260
##  9 171172173174175176177178179180|-1/-1/-1/1/1/-1/1/1/-1/-1 <int [232]>   232
## 10 281282283284285286287288289290|1/-1/-1/-1/1/-1/1/1/1/-1  <int [231]>   231
## # … with 9,906 more rows

Y ahora extraemos los pares similares

pares_candidatos <- lapply(cubetas_tbl$ids, function(x){
  combn(sort(x), 2, simplify = FALSE)}) %>% 
  flatten %>% unique %>% 
  transpose %>% lapply(as.integer) %>% as.data.frame
names(pares_candidatos) <- c('id_1','id_2')
head(pares_candidatos)

##   id_1 id_2
## 1    1    2
## 2    1    4
## 3    1    5
## 4    1    6
## 5    1    7
## 6    1    8

Ejemplo: filtrar y evaluar resultados

Y ahora evaluamos nuestros resultados. En primer lugar, el número de pares reales y de candidatos es

pares_reales <- filter(pares_tbl, dist < 0.15) %>%
                select(id_1, id_2)
nrow(pares_reales)

## [1] 179700

nrow(pares_candidatos)

## [1] 262288

Podemos evaluar con la precisión, que es el porcentaje de los pares candidatos que son reales (si este número es muy bajo, puede ser que estemos haciendo demasiado cómputo):

prec <- nrow(inner_join(pares_candidatos, pares_reales)) / 
  nrow(pares_candidatos)
prec %>% round(4)

## [1] 0.6848

Y ahora calculamos el recall o sensibilidad (porcentaje de pares similares que recuparamos):

sens <- nrow(inner_join(pares_candidatos, pares_reales)) / 
  nrow(pares_reales)
sens %>% round(4)

## [1] 0.9995

Finalmente, podemos calcular la distancia exacta entre los pares candidatos, y filtrar para obtener precisión igual a 1 (con la misma sensibilidad).

Observación: es posible, en lugar de usar vectores con dirección aleatoria \(v\) escogidos al azar como arriba (con la distribución normal), hacer menos cálculos escogiendo vectores \(v\) cuyas entradas son solamente \(1\) y \(-1\). El cálculo del producto punto es simplemente multiplicar por menos si es necesario los valores de los vectores \(x\) y sumar.

3.9 LSH para distancia euclideana.

Para distancia euclideana usamos el enfoque de proyecciones aleatorias en cubetas. La idea general es que tomamos una línea al azar en el espacio de entradas, y la dividimos en cubetas de manera uniforme. El valor hash de un punto \(x\) es el número de cubeta donde cae la proyección de \(x\).

Supogamos que tomamos como \(a\) el ancho de las cubetas. La familia de proyecciones aleatorias por cubetas es una familia \((a/2, 2a, 1/2, 1/3)\)-sensible a la localidad para la distancia euclideana.

Supongamos que dos puntos \(x\) y \(y\) tienen distancia euclideana \(d = a/2\). Si proyectamos perpendicularmente sobre la línea escogida al azar, la distancia entre las proyecciones es menor a \(a/2\), de modo la probabilidad de que caigan en la misma cubeta es al menos \(1/2\). Si la distancia es menor, entonces la probabilidad es más grande aún: 1. Si \(d(x,y)\leq a/2\) entonces \(P(f(x)=f(y))\geq 1/2\). Por otro lado, si la distancia es mayor a \(2a\), entonces la única manera de que los dos puntos caigan en una misma cubeta es que la distancia de sus proyecciones sea menor a \(a\). Esto sólo puede pasar si el ángulo entre el vector que va de \(x\) a \(y\) y la línea escogida al azar es mayor de \(60^{\circ}\) a \(90^{\circ}\). Como \(\frac{90^{\circ}-60^{\circ}}{90^{\circ}-0^{\circ}} = 1/3\), entonces la probabilidad que que caigan en la misma cubeta no puede ser más de \(1/3\). 1. Si \(d(x,y)\geq 2a\), entonces \(P(f(x)=f(y))\leq 1/3\). Escoger \(a\) para discriminar las distancias que nos interesa, y luego amplificar la familia para obtener tasas de falsos positivos y negativos que sean aceptables.

3.10 Joins por similitud

Otro uso de las técnicas del LSH nos permita hacer uniones (joins) por similitud. La idea es la siguiente:

Tenemos una tabla A, con una columna A.x que es un texto, por ejemplo, o un vector de números, etc.
Tenemos una tabla B, con una columna B.x que es del mismo tipo que A.x
Queremos hacer una unión de A con B con la llave x, de forma que queden pareados todos los elementos tales que \(sim(A.x_i, A.y_j)\).

Un ejemplo es pegar dos tablas de datos de películas de fuentes distintas mediante el título (que a veces varía en cómo está escrito, de manera que no podemos hacer un join usual), o títulos de pláticas en diferentes conferencias, etc.

Usando LSh podemos hacer un join aproximado por similitud. La idea es la misma que antes:

Calculamos cubetas de la misma forma para cada tabla (mismos hashes y bandas)
Unimos las cubetas de las dos fuentes
Los pares candidatos son todos los pares (uno de A y uno de B) que caen en la misma cubeta.

Referencias

Leskovec, Jure, Anand Rajaraman, and Jeffrey David Ullman. 2014. Mining of Massive Datasets. 2nd ed. New York, NY, USA: Cambridge University Press. http://www.mmds.org.

Mullen, Lincoln. 2016. Textreuse: Detect Text Reuse and Document Similarity. https://CRAN.R-project.org/package=textreuse.