4 Procesamiento de flujos y hashing

En esta parte supondremos que los datos se pueden representar como un flujo de tal velocidad y volumen que típicamente no es posible almacenar en memoria todo el flujo, o más en general, que para nuestros propósitos sería lento hacer queries a la base de datos resultante. Veremos técnicas simples para obtener resúmenes simples y rápidos de flujos grandes, y también veremos cómo aplicar métodos probabilísticos para filtrar o resumir ciertos aspectos de estos flujos.

Ejemplos de flujos que nos interesan son: logs generados por visitas y transacciones en sitios de internet, datos de redes de sensores, o transacciones en algún sistema.

Para analizar flujos con estas propiedades podemos hacer:

Restricción temporal: considerar ventanas de tiempo, y hacer análisis sobre los últimos datos en la ventana. Datos nuevos van reemplazando a datos anteriores, y puede ser que los datos anteriores no se respaldan (o es costoso acceder a ellos).
Resúmenes acumulados: guardamos resúmenes de los datos que podemos actualizar y utilizar para calcular características de interés en el sistema, por ejemplo: conteos simples, promedios. Algunos resúmenes son más difíciles de hacer eficientemente: por ejemplo, número de elementos únicos del flujo.
Muestreo probabilístico: Podemos diseñar muestras apropiadas para estimar cantidades que nos interesen, y sólo guardar los datos que corresponden a la muestra.
Filtrado: cómo retener para análisis elementos del flujo que satisfagan alguna propiedad de interés.

4.1 Selección de muestras y funciones hash

Dependiendo de qué nos interesa medir en un flujo podemos decidir cuáles son las unidades que es necesario muestrear. Típicamente la unidad de un flujo no corresponde a las unidades que nos interesan. Por ejemplo: en logs de sitios web, las unidades que observamos en el flujo son transacciones muy granulares (clicks, movimientos de mouse, envío de datos, etc.), pero nos interesa obtener propiedades a nivel de usuario, o sesión, etc.

Dependiendo de las unidades de muestreo apropiadas que nos interesen (por ejemplo, clientes o usuarios, transacciones, etc.) podemos diseñar distintas estrategias.

Ejemplo: transacciones

Si nos interesa estimar el promedio del tamaño de las transacciones en una ventana de tiempo dada, podemos muestrar esa ventana. Cada vez que llega una transacción, usamos un número aleatorio para decidir si lo incluimos en la muestra o no, y luego hacer nuestro análisis con las unidades seleccionadas.

library(tidyverse)

generar_trans <- function(...){
  id_num <- sample.int(10000, 1)
  monto <- rt(1, df = 5, ncp = 5000) 
  trans <- list(id = id_num, monto = monto)
  trans
}

Ahora simulamos un flujo y calculamos la mediana, con todos los datos:

set.seed(312)
trans <- map(1:100000, generar_trans) 
total_montos <- map_dbl(trans, "monto")
median(total_montos)

## [1] 5358.726

Si queremos seleccionar un \(1\%\) de las transacciones para hacer más rápido nuestro cálculo, podemos seleccionar al azar para cada elemento si lo incluímos en la muestra o no, por ejemplo:

seleccionar_rng <- function(prop = 0.01){
   runif(1) < prop
}
trans_filtradas <- keep(trans, ~ seleccionar_rng(prop = 0.01))
length(trans_filtradas)

## [1] 949

trans_filtradas %>% map_dbl("monto") %>% median

## [1] 5305.06

Este esquema simple no funciona bien cuando nuestra unidad de análisis no corresponde a las unidades del flujo, como en este ejemplo. ¿Puedes dar ejemplos?

Ejemplo: clientes

Ahora supongamos que queremos estimar el promedio de la transacción máxima por cliente en una ventana de tiempo dada. En este caso, la unidad de muestreo más simple es el cliente, y el método del ejemplo anterior es menos apropiado. Quisiéramos en lugar de eso tomar una muestra de clientes en la ventana, tomar el máximo de todas sus transacciones, y luego promediar.

En este caso, el análisis es más complicado si seleccionamos cada transacción según un número aleatorio (pues en la muestra resultante distintos clientes tendrán distintas probabilidades de inclusión, dependiendo de cuántas transacciones hagan en la ventana de tiempo).

Podemos usar una función hash del identificador único de cliente, y mapear con una función hash a un cierto número de cubetas \(1,\ldots, B\). Los clientes de la muestra son los que caen en las cubetas \(1,2,\ldots, k\), y así obtendríamos una muestra que consiste de \(k/B\) de los clientes totales que tuvieron actividad en la ventana de interés. Almacenamos todas las transacciones en la ventana de interés para los clientes seleccionados.

Con esta estrategia:

Todos los clientes que tuvieron actividad en la ventana tienen la misma probabilidad de ser seleccionados.
No es necesario buscar en una lista si el cliente está en la muestra seleccionada o no (lo cual puede ser lento, o puede ser que terminemos con muestras muy grandes o chicas).
Podemos escoger \(k\) para afinar el tamaño de muestra que buscamos.
Este método incorpora progresivamente nuevos clientes a la lista muestreada. Por ejemplo, si la cantidad de clientes está creciendo, entonces el número de clientes muestreados crecerá de manera correspondiente. Podemos empezar escogiendo \(A\) de \(B\) cubetas (con \(B\) grande), y si la muestra de cientes excede el tamaño planeado, reducir a \(A-1\) cubetas, y así sucesivamente.

Primero veamos el resultado cuando utilizamos todos los clientes de la ventana de tiempo:

sprintf("Número de clientes: %i", length(unique(map_int(trans, "id"))))

## [1] "Número de clientes: 9997"

trans_df <- trans %>% bind_rows() 
mediana_max <- trans_df %>% 
  group_by(id) %>% 
  summarise(monto_max = max(monto)) %>%
  pull(monto_max) %>% median 
sprintf("Mediana de máximo monto: %.1f", mediana_max)

## [1] "Mediana de máximo monto: 9622.1"

¿Cómo funciona si quisiéramos usar una muestra? Usamos una función hash y repartimos en \(10\) cubetas (deberíamos obtener alrededor del \(10\%\) de los clientes). Seleccionamos una sola cubeta y la usamos para resumir:

seleccionar <- function(id){
  ((28*id + 110) %% 117) %% 10  == 0
}

trans_filtradas <- keep(trans, ~ seleccionar(.x$id))
sprintf("Número de clientes: %i", length(unique(map_int(trans_filtradas, "id"))))

## [1] "Número de clientes: 1026"

trans_df <- trans_filtradas %>% bind_rows() 
mediana_max <- trans_df %>% 
  group_by(id) %>% 
  summarise(monto_max = max(monto)) %>%
  pull(monto_max) %>% median 
sprintf("Mediana de máximo monto: %.1f", mediana_max)

## [1] "Mediana de máximo monto: 9658.2"

Sin embargo, esto no funciona si seleccionamos al azar las transacciones. En este caso, obtenemos una mala estimación con sesgo alto:

trans_filtradas <- keep(trans, ~ seleccionar_rng(prop = 0.10))
length(trans_filtradas)

## [1] 9878

trans_df <- trans_filtradas %>% bind_rows() 
mediana_max_incorrecta <- trans_df %>% 
  group_by(id) %>% 
  summarise(monto_max = max(monto)) %>%
  pull(monto_max) %>% median 
sprintf("Mediana de máximo monto: %.1f", mediana_max_incorrecta)

## [1] "Mediana de máximo monto: 5923.5"

Observación:

En este último ejemplo, para cada usuario sólo muestreamos una fracción de sus transacciones. En algunos casos, no muestreamos el máximo, y esto produce que la estimación esté sesgada hacia abajo.
Para un enfoque más general (por ejemplo id’s que son cadenas), podemos usar alguna función hash de cadenas.

4.2 Contando elementos diferentes en un flujo.

Supongamos que queremos contar el número de elementos diferentes que aparecen en un flujo, por ejemplo, cuántos usuarios únicos tiene un sitio (según un identificador como login, cookies, etc).

Entonces tenemos que tomar cada dato con un identificador que llega del flujo, y consultar para ver si hemos visto ese identificador o no. Si es nuevo, lo agregamos a la estructura de datos y agregamos 1 a nuestro conteo. Si en la consulta encontramos el identificador, entonces no hacemos nada. Si el flujo es grande y el número de únicos es grande, entonces mantener una estructura de datos identificador puede ser costoso en memoria.

Si lo único que nos interesa es contar rápidamente cuántos únicos hemos visto (aproximadamente), entonces podemos usar algoritmos probabilísticos que utilizan muy poca memoria y tiempo.

4.2.1 El algoritmo de Flajolet-Martin

Este es uno de los primeros algoritmos para atacar este problema, y se basa en el uso de funciones hash. La referencia básica es este (paper)[http://algo.inria.fr/flajolet/Publications/FlFuGaMe07.pdf], (Flajolet et al. 2007)

La idea básica del algoritmo de Flajolet-Martin se basa en la siguiente observación:

Si escogemos funciones hash que mapeen elementos del conjunto del flujo a una sucesión de bits suficientemente grande, conforme haya más elementos distintos en el flujo observaremos más valores hash distintos, y en consecuencia, es más probable observar sucesiones de bits con características especiales.

La característica especial que se explota en este algoritmo es el número de ceros que hay al final de las cadenas de bits.

Ejemplo

Consideramos una función hash (para cadenas) que da la representación binaria del hash:

hash_gen <- function(seed){
  function(x){
    digest::digest2int(x, seed = seed) %>% intToBits()
  }
}
set.seed(5451)
hash_1 <- hash_gen(seed = 123333)
hash_2 <- hash_gen(seed = 56004)
hash_1("7yya71872fae")

##  [1] 01 01 01 01 01 01 00 00 00 01 01 00 00 00 01 00 00 00 01 01 00 01 00 01 00
## [26] 01 00 00 01 01 01 00

Y ahora hacemos una función para contar el número 0’s consecutivos en la cola de esta representación:

long_cola <- function(bits){
  bits %>% which.max - 1   
}
hash_1("7yya71872fae") %>% long_cola

## [1] 0

La idea es que conforme veamos más elementos distintos, es más probable observar que la cola de ceros es un número más grande. Como la función hash que usamos es determinista, los elementos ya vistos no contribuyen a hacer crecer a este número.

Discusión

Antes se seguir, hacemos la siguiente observación: Si consideramos los bits de cada nuevo elemento como aleatorios:

La probabilidad de que observemos una cola de 0’s de tamaño al menos \(m\) es \(2^{-m}\), para \(m \geq 1\)
Supongamos que tenemos una sucesión de \(n\) candidatos del flujo distintos. La probabilidad de que ninguno tenga una cola de ceros de tamaño mayor a \(m\) es igual a \[\begin{equation} (1-2^{-m})^{n} \tag{4.1} \end{equation}\]

Que también es la probabilidad de que el máximo de las colas sea menor a \(m\). Reescribimos como

\[((1-2^{-m})^{2^m})^{\frac{n}{2^{m}}}. \]

Ahora notamos que la expresión de adentro se escribe (si \(m\) no es muy chica) como \[P(max < m) = (1-2^{-m})^{2^m} = (1-1/t)^t\approx e^{-1}\approx 0.3678\]

Si \(n\) es mucho más grande que \(2^m\), entonces la expresión (4.1) es chica, y tiende a \(0\) conforme \(n\) crece.
Si \(2^m\) es mucho más grande que \(n\), entonces la expresión (4.1) es cercana a \(1\), y tiende a \(1\) conforme \(m\) crece.
Así que para una sucesión de \(n\) elementos distintos, es poco probable observar que la longitud \(m\) de la máxima cola de 0’s consecutivos es tal que \(2^m\) es mucho más grande que \(n\) o mucho más chica que \(n\). Abajo graficamos unos ejemplos:

proba_cola <- function(distintos, r){
  #proba de que el valor máximo de cola de 0's sea r
  al_menos_r <- 1- (1-0.5^r) ^ distintos 
  no_mas_de_r <- 1 - (1-0.5 ^ {r+1}) ^ distintos
  prob <-  al_menos_r - no_mas_de_r 
  prob
}
df_prob <- data_frame(n = c(2^5, 2^10, 2^20)) %>%
  mutate(probas = map(n, function(n){ 
    m <- 1:30
    probas <- sapply(m, function(x){proba_cola(n, x)})
    tibble(m = m, probas = probas)
    })) %>%
  unnest

## Warning: `data_frame()` is deprecated, use `tibble()`.
## This warning is displayed once per session.

## Warning: `cols` is now required.
## Please use `cols = c(probas)`

ggplot(df_prob, aes(x = 2^m, y = probas, colour = factor(n))) + geom_line() +
   ylab("Probabilidad de máxima cola de 0s") +
    scale_x_log10(breaks=10 ^ (1:7))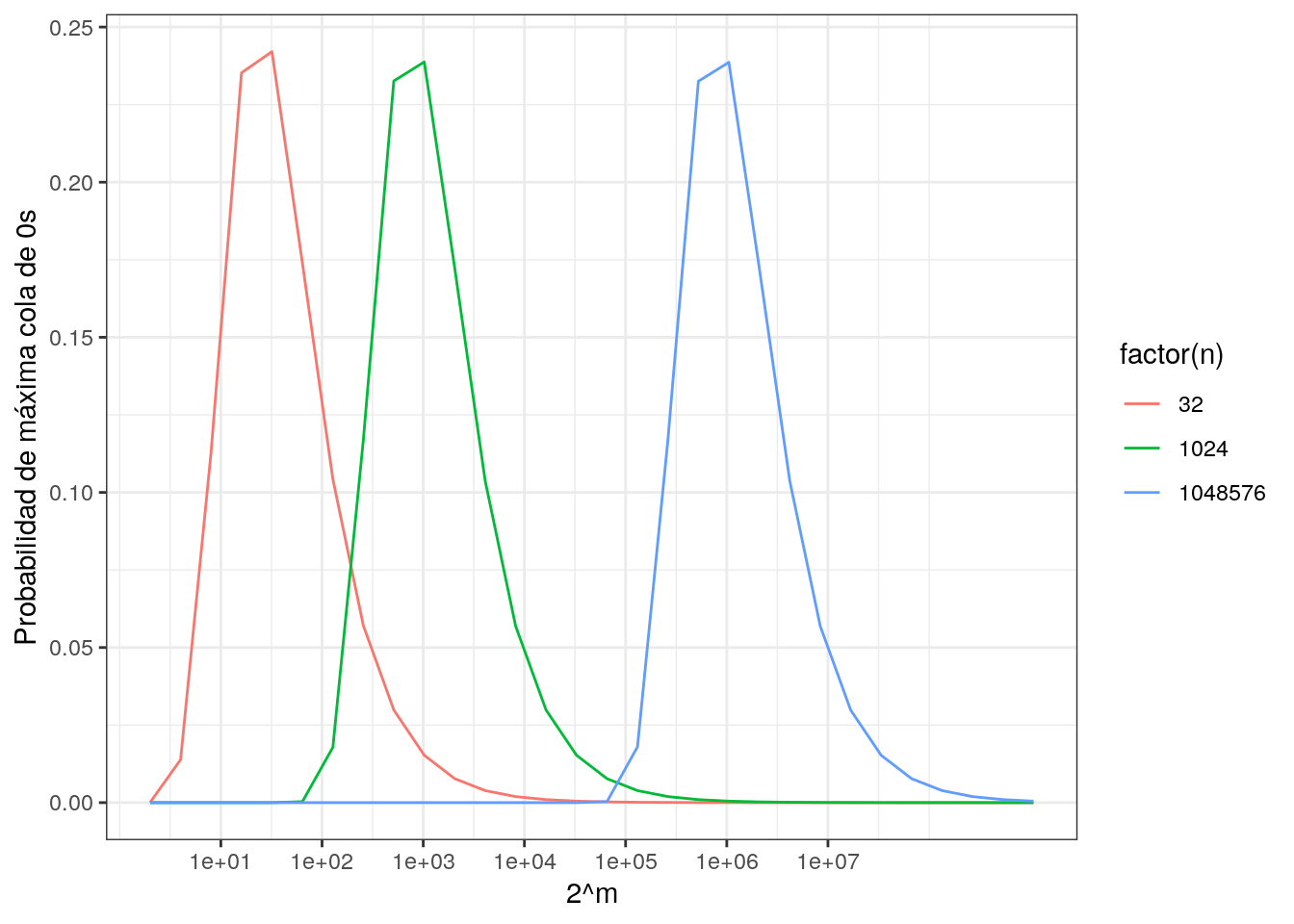

c(2^5, 2^10, 2^20)

## [1]      32    1024 1048576

Y ahora podemos probar cómo se ve la aproximación con dos funciones hash diferentes:

n <- 10000
set.seed(9923)
tail_hash_1 <- compose(long_cola, hash_1)
tail_hash_2 <- compose(long_cola, hash_2)
df <- data_frame(num_distintos = 1:n) %>%
      mutate(id = as.character(sample.int(52345678, n))) %>%
      mutate(tail_1 = map_dbl(id, tail_hash_1)) %>%
      mutate(tail_2 = map_dbl(id, tail_hash_2))
df

## # A tibble: 10,000 x 4
##    num_distintos id       tail_1 tail_2
##            <int> <chr>     <dbl>  <dbl>
##  1             1 27965680      2      0
##  2             2 27866260      0      0
##  3             3 27354527      0      0
##  4             4 3174805       3      1
##  5             5 42728100      1      3
##  6             6 45922157      4      1
##  7             7 10060939      0      0
##  8             8 34627594      0      0
##  9             9 28127141      0      0
## 10            10 19593935      8      2
## # … with 9,990 more rows

Y ahora calculamos el máximo acumulado

df <- df %>% mutate(max_tail_1 = cummax(tail_1), max_tail_2 = cummax(tail_2))
tail(df)

## # A tibble: 6 x 6
##   num_distintos id       tail_1 tail_2 max_tail_1 max_tail_2
##           <int> <chr>     <dbl>  <dbl>      <dbl>      <dbl>
## 1          9995 686071        1      6         13         12
## 2          9996 44308878      0      1         13         12
## 3          9997 50343611      3      1         13         12
## 4          9998 18117113      1      0         13         12
## 5          9999 38596740      0      1         13         12
## 6         10000 46515085      0      3         13         12

ggplot(df, aes(x = num_distintos, y = 2^max_tail_1)) + 
  geom_abline(slope=1, intercept = 0, colour = "red") + 
  geom_point() +
  scale_x_log10() + scale_y_log10()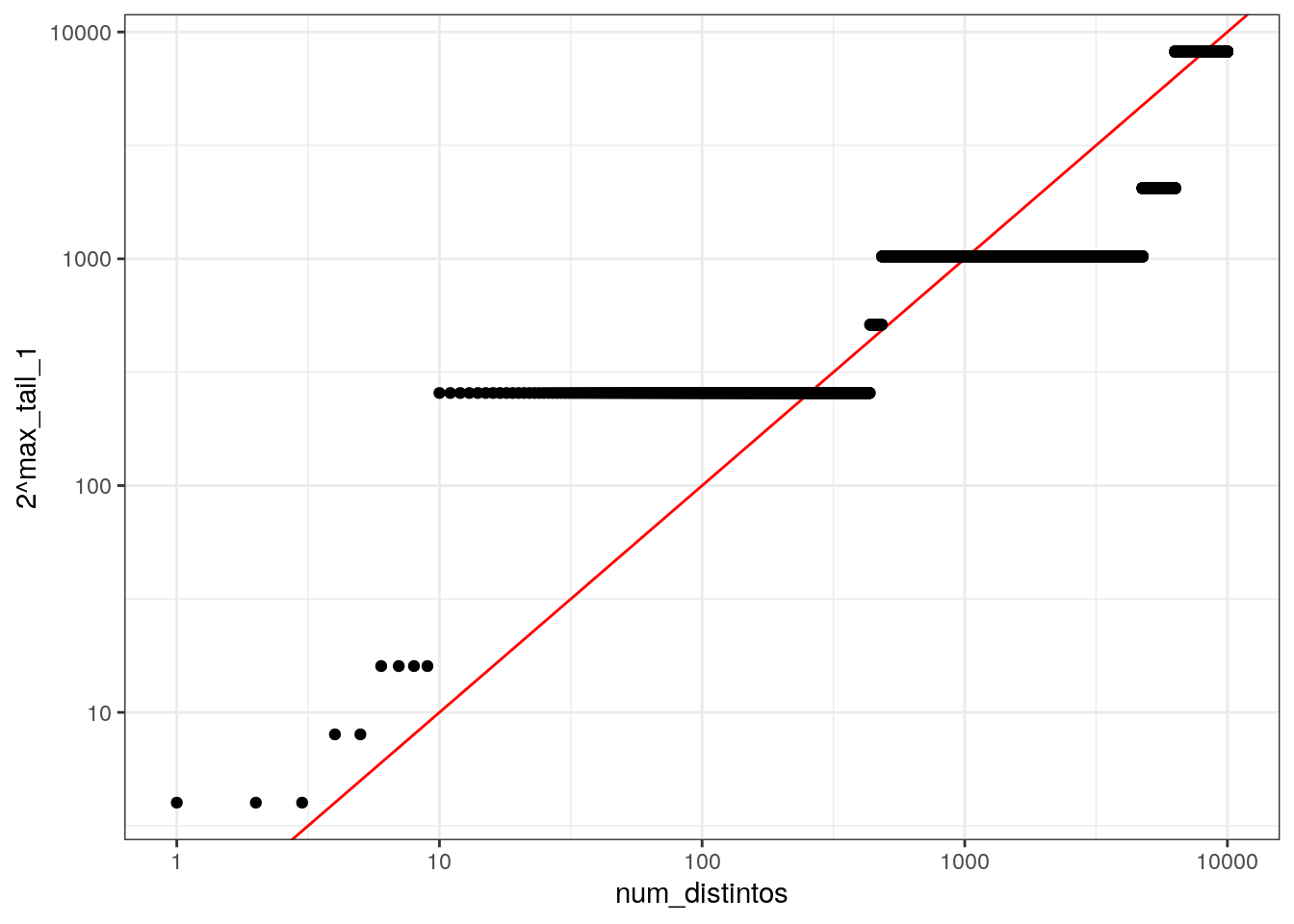

ggplot(df, aes(x = num_distintos, y = 2^max_tail_2)) + 
  geom_abline(slope=1, intercept = 0, colour = "red") + 
  geom_point() +
  scale_x_log10() + scale_y_log10()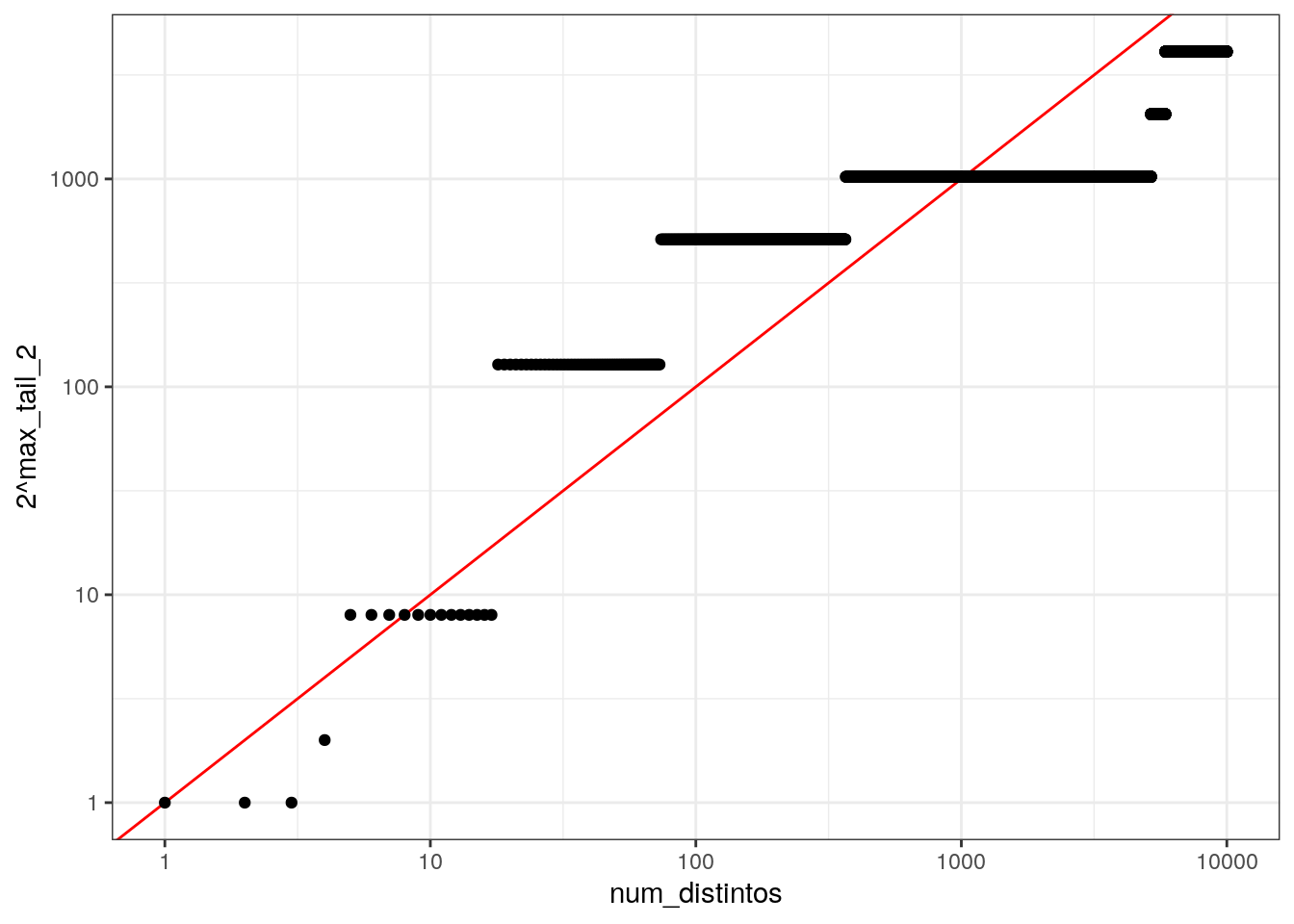

Nótese que las gráficas están en escala logarítmica, así que la estimación no es muy buena en términos absolutos si usamos un solo hash. Sin embargo, confirmamos que la longitud máxima de las colas de 0’s crece con el número de elementos distintos en el flujo.

4.3 Combinación de estimadores, Hyperloglog

Como vimos en los ejemplos anteriores, la estimación de Flajolet-Martin tiene dos debilidades: varianza alta, y el hecho de que el único resultado que puede dar es una potencia de \(2\).

Podemos usar varias funciones hash y combinarlas de distintas maneras para obtener una mejor estimación con menos varianza.

La primera idea, que puede ser promediar los valores obtenidos de varias funciones hash, requeriría muchas funciones hash por la varianza alta del estimador, de modo que esta opción no es muy buena. En nuestro ejemplo anterior, la desviación estándar del estimador es:

df_prob %>% group_by(n) %>%
  mutate(media = sum((2^m)*probas)) %>%
  summarise(desv_est = sqrt(sum(probas*(2^m-media)^2)))

## # A tibble: 3 x 2
##         n  desv_est
##     <dbl>     <dbl>
## 1      32   185363.
## 2    1024  1048521.
## 3 1048576 33061240.

Usar la mediana para evitar la posible variación grande de este estimador tiene la desventaja de que al final obtenemos una estimación de la forma \(2^R\), que también tiene error grande.
Una mejor alternativa es utilizar la recomendación de (Leskovec, Rajaraman, and Ullman 2014), que consiste en agrupar en algunas cubetas las funciones hash, promediar los estimadores \(2^{R_i}\) dentro de cada cubeta, y luego obtener la mediana de las cubetas.

4.3.1 Hyperloglog

Esta solución (referida en el paper anterior, (Flajolet et al. 2007)) es una de las más utilizadas y refinadas. En primer lugar:

Para hacer las cubetas usamos los mismos bits producidos por el hash (por ejemplo, los primeros \(p\) bits). Usamos los últimos bits del mismo hash para calcular la longitud de las colas de 0’s.
Usamos promedio armónico de los valores máximos de cada cubeta (más robusto a valores grandes y atípicos, igual que la media geométrica).
Intuitivamente, cuando dividimos en \(m\) cubetas un flujo de \(n\) elementos, cada flujo tiene aproximadamente \(n/m\) elementos. Como vimos arriba, lo más probable es que la cola máxima en cada cubeta sea aproximadamente \(\log_2(n/m)\). El promedio armónico \(a\) de \(m\) cantidades \((n/m)\) de esta cantidad entonces debería ser del orden en \(n/m\), así que la estimación final de la cardinalidad del flujo completo es \(ma\) (el número de cubetas multiplicado por el promedio armónico).
Existen varias correcciones adicionales para mejorar su error en distintas circunstancias (dependiendo del número de elemntos únicos que estamos contando, por ejemplo). Una típica es multiplicar por \(0.72\) el resultado de los cálculos anteriores para corregir sesgo multiplicativo (ver referencia de Flajolet).

Veamos una implementación simplificada (nota: considerar spark para hacer esto, que incluye una implementación rápida del hyperloglog), usando las funciones hash que construimos arriba.

Primero construimos la función que separa en cubetas, y una nueva función para calcular la longitud de la cola una vez que quitamos los bits que indican la cubeta:

cubeta_bits <- 7
m <- 2^cubeta_bits
long_cola_lead <- function(bits){
  rev(bits) %>% which.max %>% as.integer
}
id <- "7yyda998d"
hash_1(id)

##  [1] 00 00 01 01 01 00 00 01 00 00 00 01 01 00 00 00 00 00 01 01 00 00 00 00 00
## [26] 01 00 01 01 01 01 00

hash_1(id) %>% long_cola_lead

## [1] 2

cubeta <- function(bits){
  paste0(as.character(bits[1:cubeta_bits]), collapse = "")
}
hash_1(id) %>% cubeta

## [1] "00000101010000"

Simulamos unos datos y calculamos la cubeta para cada dato:

n <- 10000
hash_1 <- hash_gen(seed= 292811)
df <- data_frame(num_distintos = 1:n) %>%
      mutate(id = as.character(sample.int(52345678, n, replace = FALSE))) %>%
      mutate(hash = map(id, hash_1)) %>%
      mutate(cubeta = map_chr(hash, cubeta))
df

## # A tibble: 10,000 x 4
##    num_distintos id       hash    cubeta        
##            <int> <chr>    <list>  <chr>         
##  1             1 17713053 < [32]> 00000100000001
##  2             2 25082957 < [32]> 01000100000101
##  3             3 49206761 < [32]> 01000101000000
##  4             4 27855801 < [32]> 01010100010000
##  5             5 48241424 < [32]> 00000000000000
##  6             6 39205056 < [32]> 01010001000000
##  7             7 17780584 < [32]> 01010001010001
##  8             8 16443873 < [32]> 00000100010100
##  9             9 27196849 < [32]> 01000100010101
## 10            10 31278701 < [32]> 00000101010001
## # … with 9,990 more rows

Y calculamos la longitud de la cola:

df <- df %>% mutate(tail = map_int(hash, long_cola_lead))
df

## # A tibble: 10,000 x 5
##    num_distintos id       hash    cubeta          tail
##            <int> <chr>    <list>  <chr>          <int>
##  1             1 17713053 < [32]> 00000100000001     1
##  2             2 25082957 < [32]> 01000100000101     4
##  3             3 49206761 < [32]> 01000101000000     1
##  4             4 27855801 < [32]> 01010100010000     2
##  5             5 48241424 < [32]> 00000000000000     3
##  6             6 39205056 < [32]> 01010001000000     1
##  7             7 17780584 < [32]> 01010001010001     1
##  8             8 16443873 < [32]> 00000100010100     1
##  9             9 27196849 < [32]> 01000100010101     1
## 10            10 31278701 < [32]> 00000101010001     1
## # … with 9,990 more rows

Ahora vemos cómo calcular nuestra estimación. cuando hay \(50\) mil distintos, calculamos máximo por cubeta

resumen_50 <- df %>% filter(num_distintos <= 50000) %>% 
    group_by(cubeta) %>% 
    summarise(tail_max = max(tail))
resumen_50

## # A tibble: 128 x 2
##    cubeta         tail_max
##    <chr>             <int>
##  1 00000000000000        7
##  2 00000000000001       10
##  3 00000000000100        7
##  4 00000000000101        5
##  5 00000000010000        7
##  6 00000000010001        7
##  7 00000000010100        8
##  8 00000000010101        7
##  9 00000001000000        8
## 10 00000001000001        6
## # … with 118 more rows

Y luego calculamos la media armónica y reescalamos para obtener:

armonica <- function(x) 1/mean(1/x)
0.72 * m * armonica(2 ^ resumen_50$tail_max)

## [1] 10352.09

Y esta es nuestra estimación de únicos en el momento que el verdadero valor es igual a \(50000\).

Podemos ver cómo se desempeña la estimación conforme nuevos únicos van llegando (el siguiente cálculo son necesarias algunas manipulaciones para poder calcular el estado del estimador a cada momento);

res <- df %>% spread(cubeta, tail, fill = 0) %>%
        gather(cubeta, tail, -num_distintos, -id, -hash) %>%
        select(num_distintos, cubeta, tail) 
res_2 <- res %>% 
      group_by(cubeta) %>%
      arrange(num_distintos) %>%
      mutate(tail_max = cummax(tail)) %>%
      group_by(num_distintos) %>%
      summarise(estimador_hll = 0.72*(m*armonica(2^tail_max)))
ggplot(res_2 %>% filter(num_distintos > 100),
       aes(x = num_distintos, y = estimador_hll)) + geom_line() +
  geom_abline(slope = 1, colour ='red')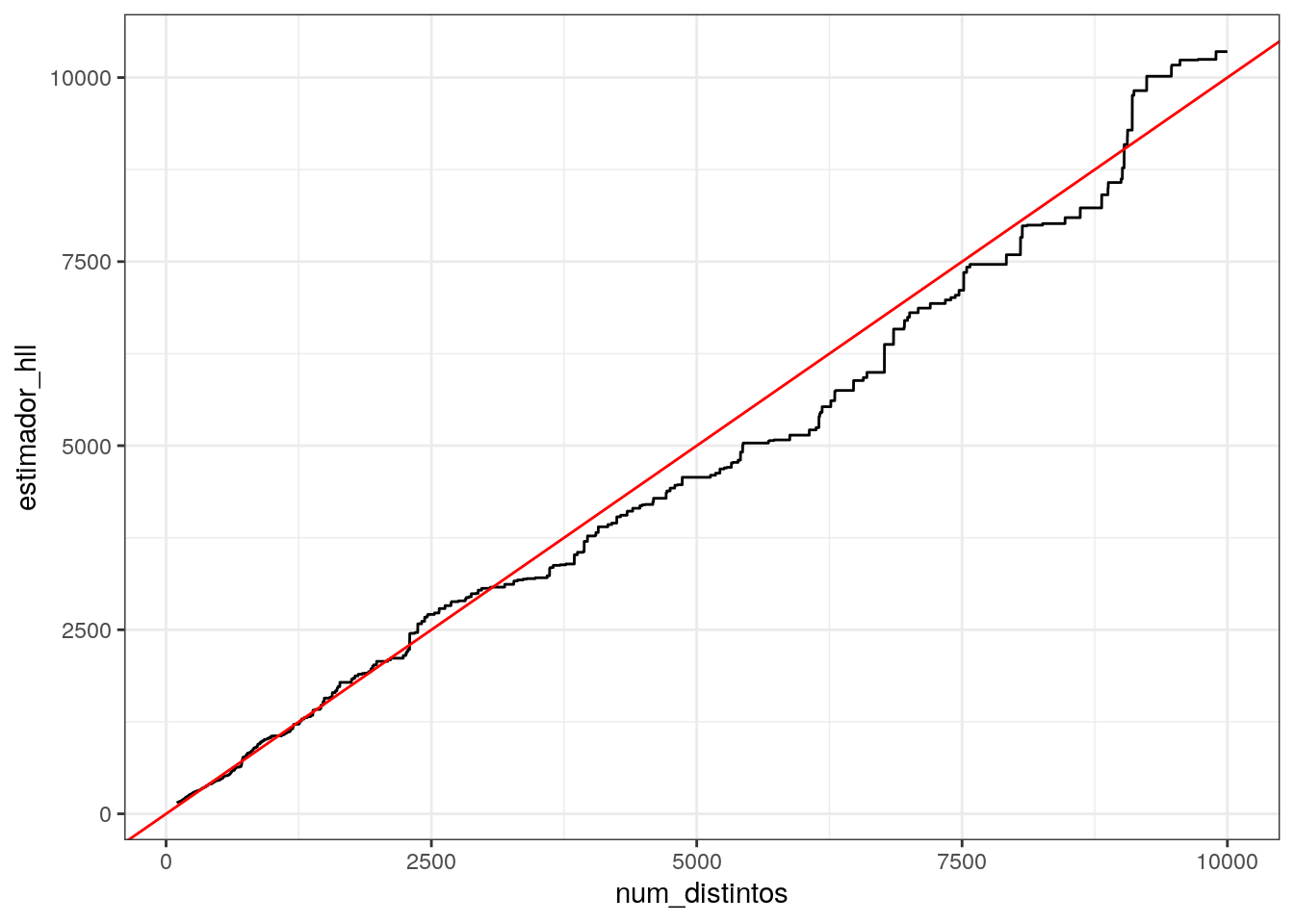

Finalmente, examinamos el error relativo:

quantile(1 - res_2$estimador_hll/res_2$num_distintos, probs=c(0.1, 0.5, .9))

##         10%         50%         90% 
## -0.06820853  0.04315869  0.10701737

Observaciones - Ver también este paper para mejoras del hyperloglog (por ejemplo, si es posible es preferible usar hashes de \(64\) bits en lugar de \(32\)).

El error relativo teórico del algoritmo (con algunas mejoras que puedes ver en los papers citados) es de \(1.04/\sqrt{m}\), donde \(m\) es el número de cubetas, así que más cubetas mejoran el desempeño.
Las operaciones necearias son: aplicar la función hash, calcular cubeta, y actualizar el máximo de las cubetas. La única estructura que es necesario mantener es los máximos de las colas dentro de cada cubeta que se actualiza secuencialmente.

4.3.2 Implementación de spark

La implementación de hyperloglog en Spark se puede utilizar con el siguiente código:

library(sparklyr)

## 
## Attaching package: 'sparklyr'

## The following object is masked from 'package:purrr':
## 
##     invoke

sc <- spark_connect(master = "local") # esto normalmente no lo hacemos desde R
df_tbl <- copy_to(sc, df %>% select(num_distintos, id))
df_tbl %>%
  summarise(unicos_hll = approx_count_distinct(id)) # error estándar relativo 0.05

## # Source: spark<?> [?? x 1]
##   unicos_hll
##        <dbl>
## 1      10084

spark_disconnect_all()

## [1] 1

Referencias

Flajolet, Philippe, Éric Fusy, Olivier Gandouet, and et al. 2007. “Hyperloglog: The Analysis of a Near-Optimal Cardinality Estimation Algorithm.” In IN Aofa ’07: PROCEEDINGS of the 2007 International Conference on Analysis of Algorithms.

Leskovec, Jure, Anand Rajaraman, and Jeffrey David Ullman. 2014. Mining of Massive Datasets. 2nd ed. New York, NY, USA: Cambridge University Press. http://www.mmds.org.