9 Representación de palabras y word2vec
En esta parte empezamos a ver los enfoques más modernos (redes neuronales) para construir modelos de lenguajes y resolver tareas de NLP. Se trata de modelos de lenguaje que incluyen más estructura, son más fáciles de regularizar y de ampliar si es necesario para incluir dependencias de mayor distancia. El método de conteo/suavizamiento de ngramas es simple y funciona bien para algunas tareas, pero podemos construir mejores modelos con enfoques más estructurados, y con más capacidad para aprender aspectos más complejos del lenguaje natural.
Un enfoque que recientemente se ha vuelto más importante es el de redes neuronales. Si \(w=w_1w_2\cdots w_N\) es una frase, y las \(w\) representan palabras, recordemos que un modelo de lenguaje con dependencia de \(n\)-gramas consiste de las probabilidades
\[P(w_t | w_{t-1} w_{t-2} \cdots w_{t-n+1}),\]
(n=2, bigramas, n=3 trigramas, etc.)
Y vimos que tenemos problemas cuando observamos sucesiones que no vimos en el corpus de entrenamiento. Este problema se puede “parchar” utilizando técnicas de suavizamiento. Aún para colecciones de entrenamiento muy grandes tenemos que lidiar con este problema.
Podemos tomar un enfoque más estructurado pensando en representaciones “distribucionales” de palabras:
- Asociamos a cada palabra en el vocabulario un vector numérico con \(d\) dimensiones, que es su representación distribuida.
- Expresamos la función de probabilidad como combinaciones de las representaciones vectoriales del primer paso.
- Aprendemos (máxima verosimiltud/con o sin regularización) simultáneamente los vectores y la manera de combinar estos vectores para producir probabilidades.
La idea de este modelo es entonces subsanar la relativa escasez de datos (comparado con todos los trigramas que pueden existir) con estructura. Sabemos que esta es una buena estrategia si la estrucutura impuesta es apropiada.
El objeto es entonces abstraer características de palabras (mediante estas representaciones) intentando no perder mucho de su sentido original, lo que nos permite conocer palabras por su contexto, aún cuando no las hayamos observado antes.
Ejemplo
¿Cómo puede funcionar este enfoque? Por ejemplo, si vemos la frase “El gato corre en el jardín”, sabemos que una frase probable debe ser también “El perro corre en el jardín”, pero quizá nunca vimos en el corpus la sucesión “El perro corre”. La idea es que como “perro” y “gato” son funcionalmente similares (aparecen en contextos similares en otros tipos de oraciones como el perro come, el gato come, el perro duerme, este es mi gato, etc.), un modelo como el de arriba daría vectores similares a “perro” y “gato”, pues aparecen en contextos similares. Entonces el modelo daría una probabilidad alta a “El perro corre en el jardín”.
9.1 Modelo de red neuronal
Podemos entonces construir una red neuronal con 2 capas ocultas como sigue (segimos (Bengio et al. 2003), una de las primeras referencias en usar este enfoque). Usemos el ejemplo de trigramas:
- En la primera capa oculta, tenemos un mapeo de las entradas \(w_1,\ldots, w_{n-1}\) a \(x=C(w_1),\ldots, C(w_{n-1})\), donde \(C\) es una función que mapea palabras a vectores de dimensión \(d\). \(C\) también se puede pensar como una matriz de dimensión \(|V|\) por \(d\). En la capa de entrada,
\[w_{n-2},w_{n-1} \to x = (C(w_{n-2}), C(w_{n-1})).\]
- En la siguiente capa oculta tenemos una matriz de pesos \(H\) y la función logística (o tangente hiperbólica) \(\sigma (z) = \frac{e^z}{1+e^z}\), como en una red neuronal usual.
En esta capa calculamos \[z = \sigma (a + Hx),\] que resulta en un vector de tamaño \(h\).
- La capa de salida debe ser un vector de probabilidades sobre todo el vocabulario \(|V|\). En esta capa tenemos pesos \(U\) y hacemos \[y = b + U\sigma (z),\] y finalmente usamos softmax para tener probabilidades que suman uno: \[p_i = \frac{\exp (y_i) }{\sum_j exp(y_j)}.\]
En el ajuste maximizamos la verosimilitud:
\[\sum_t \log \hat{P}(w_{t,n}|w_{t,n-2}w_{t-n-1}) \]
La representación en la referencia (Bengio et al. 2003) es:
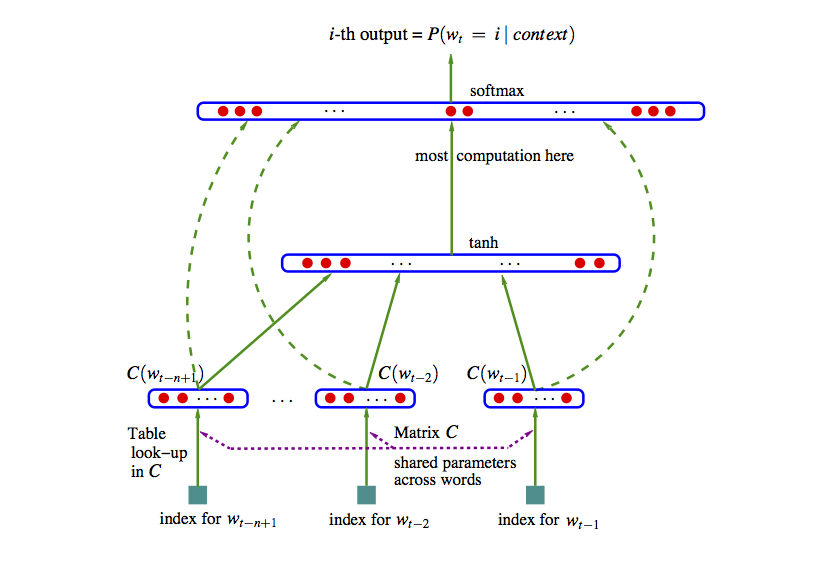
Imagen
Esta idea original ha sido explotada con éxito, aunque sigue siendo intensivo en cómputo ajustar un modelo como este. Nótese que el número de parámetros es del orden de \(|V|(nm+h)\), donde \(|V|\) es el tamaño del vocabulario (decenas o cientos de miles), \(n\) es 3 o 4 (trigramas, 4-gramas), \(m\) es el tamaño de la representacion (cientos) y \(h\) es el número de nodos en la segunda capa (también cientos o miles). Esto resulta en el mejor de los casos en modelos con miles de millones de parámetros. Adicionalmente, hay algunos cálculos costosos, como el softmax (donde hay que hacer una suma sobre el vocabulario completo). En el paper original se propone descenso estocástico.
Ejemplo
Veamos un ejemplo chico de cómo se vería el paso feed-forward de esta red. Supondremos en este ejemplo que los sesgos \(a,b\) son iguales a cero para simplificar los cálculos.
Consideremos que el texto de entrenamiento es “El perro corre. El gato corre. El león corre. El león ruge.”
En este caso, nuestro vocabulario consiste de los 8 tokens \(<s>\), el, perro, gato, león, corre, caza \(</s>\). Consideremos un modelo con \(d=2\) (representaciones de palabras en 2 dimensiones), y consideramos un modelo de trigramas.
Nuestra primera capa es una matriz \(C\) de tamaño \(2\times 8\), es decir, un vector de tamaño 2 para cada palabra. Por ejemplo, podríamos tener
library(tidyverse)
set.seed(63)
C <- round(matrix(rnorm(16, 0, 0.1), 2, 8), 2)
colnames(C) <- c("_s_", "el", "perro", "gato", "león", "corre", "caza", "_ss_")
rownames(C) <- c("d_1", "d_2")
C## _s_ el perro gato león corre caza _ss_
## d_1 0.13 0.05 0.05 0.04 -0.17 0.04 0.03 -0.02
## d_2 -0.19 -0.19 -0.11 0.01 0.04 -0.01 0.02 0.02En la siguiente capa consideremos que usaremos, arbitrariamente, \(h=3\) unidades. Como estamos considerando bigramas, necesitamos una entrada de tamaño 4 (representación de un bigrama, que son dos vectores de la matriz \(C\))
## [,1] [,2] [,3] [,4]
## [1,] -0.04 0.12 -0.09 0.18
## [2,] 0.09 0.10 0.06 0.08
## [3,] 0.10 -0.08 -0.07 -0.13Y la última capa es la del vocabulario. Son entonces 8 unidades, con 3 entradas cada una. La matriz de pesos es:
U <- round(matrix(rnorm(24, 0, 0.1), 8, 3), 2)
rownames(U) <- c("_s_", "el", "perro", "gato", "león", "corre", "caza", "_ss_")
U## [,1] [,2] [,3]
## _s_ 0.05 -0.15 -0.30
## el 0.01 0.16 0.15
## perro -0.14 0.10 0.05
## gato 0.04 0.09 0.12
## león 0.06 -0.03 0.02
## corre -0.01 0.00 -0.02
## caza 0.10 0.00 0.06
## _ss_ 0.07 -0.10 0.01Ahora consideremos cómo se calcula el objetivo con los datos de entrenamiento. El primer trigrama es (_s_, el, perro). La primera capa entonces devuelve los dos vectores correspondientes a cada palabra (concatenado):
## d_1 d_2 d_1 d_2
## 0.13 -0.19 0.05 -0.19La siguiente capa es:
## [,1]
## [1,] 0.4833312
## [2,] 0.4951252
## [3,] 0.5123475Y la capa final da
## [,1]
## _s_ -0.203806461
## el 0.160905460
## perro 0.007463525
## gato 0.125376210
## león 0.024393066
## corre -0.015080262
## caza 0.079073967
## _ss_ -0.010555858Y aplicamos softmax para encontrar las probabilidades
## [,1]
## _s_ 0.09931122
## el 0.14301799
## perro 0.12267376
## gato 0.13802588
## león 0.12476825
## corre 0.11993917
## caza 0.13178067
## _ss_ 0.12048306Y la probabilidad es entonces
## perro
## 0.1226738Cuya log probabilidad es
## perro
## -2.098227Ahora seguimos con el siguiente trigrama, que es “(el, perro, corre)”. Necesitamos calcular la probabilidad de corre dado el contexto “el perro”. Repetimos nuestro cálculo:
## d_1 d_2 d_1 d_2
## 0.05 -0.19 0.05 -0.11## [,1]
## [1,] 0.4877275
## [2,] 0.4949252
## [3,] 0.5077494## [,1]
## _s_ -0.202177217
## el 0.160227709
## perro 0.006598141
## gato 0.124982290
## león 0.024570880
## corre -0.015032262
## caza 0.079237709
## _ss_ -0.010274101## [,1]
## _s_ 0.09947434
## el 0.14292280
## perro 0.12256912
## gato 0.13797317
## león 0.12479193
## corre 0.11994636
## caza 0.13180383
## _ss_ 0.12051845Y la probabilidad es entonces
## corre
## -2.120711Sumando, la log probabilidad es:
## perro
## -4.218937y continuamos con los siguientes trigramas del texto de entrenamiento. Creamos una función
feed_fow_p <- function(trigrama, C, H, U){
trigrama <- strsplit(trigrama, " ", fixed = TRUE)[[1]]
capa_1 <- c(C[, trigrama[1]], C[, trigrama[2]])
capa_2 <- sigma(H %*% capa_1)
y <- U %*% capa_2
p <- exp(y)/sum(exp(y)) %>% as.numeric()
p
}
feed_fow_trigrama <- function(trigrama, C, H, U) {
p <- feed_fow_p(trigrama, C, H, U)
trigrama_s <- strsplit(trigrama, " ", fixed = TRUE)[[1]]
log(p)[trigrama_s[3], 1]
}Y ahora aplicamos a todos los trigramas:
texto_entrena <- c("_s_ el perro corre _ss_", " _s_ el gato corre _ss_", " _s_ el león corre _ss_",
"_s_ el león caza _ss_", "_s_ el gato caza _ss_")
entrena_trigramas <- map(texto_entrena,
~tokenizers::tokenize_ngrams(.x, n = 3)[[1]]) %>%
flatten %>% unlist
entrena_trigramas## [1] "_s_ el perro" "el perro corre" "perro corre _ss_" "_s_ el gato"
## [5] "el gato corre" "gato corre _ss_" "_s_ el león" "el león corre"
## [9] "león corre _ss_" "_s_ el león" "el león caza" "león caza _ss_"
## [13] "_s_ el gato" "el gato caza" "gato caza _ss_"## [1] -31.21475Ahora piensa como harías más grande esta verosimilitud. Observa que “perro”, “gato” y “león”" están comunmente seguidos de “corre”. Esto implica que nos convendría que hubiera cierta similitud entre los vectores de estas tres palabras, por ejemplo:
C_1 <- C
indices <- colnames(C) %in% c("perro", "gato", "león")
C_1[1, indices] <- 3.0
C_1[1, !indices] <- -1.0
C_1## _s_ el perro gato león corre caza _ss_
## d_1 -1.00 -1.00 3.00 3.00 3.00 -1.00 -1.00 -1.00
## d_2 -0.19 -0.19 -0.11 0.01 0.04 -0.01 0.02 0.02La siguiente capa queremos que extraiga el concepto “animal” en la palabra anterior, o algo similar, así que podríamos poner en la unidad 1:
## [,1] [,2] [,3] [,4]
## [1,] 0.00 0.00 5.00 0.00
## [2,] 0.09 0.10 0.06 0.08
## [3,] 0.10 -0.08 -0.07 -0.13Nótese que la unidad 1 de la segunda capa se activa cuando la primera componente de la palabra anterior es alta. En la última capa, podríamos entonces poner
## [,1] [,2] [,3]
## _s_ 0.05 -0.15 -0.30
## el 0.01 0.16 0.15
## perro -0.14 0.10 0.05
## gato 0.04 0.09 0.12
## león 0.06 -0.03 0.02
## corre 4.00 -2.00 -2.00
## caza 4.20 -2.00 -2.00
## _ss_ 0.07 -0.10 0.01que captura cuando la primera unidad se activa. Ahora el cálculo completo es:
## [1] -23.53883Y logramos aumentar la verosimilitud considerablemente. Compara las probabilidades:
## [,1]
## _s_ 0.09947434
## el 0.14292280
## perro 0.12256912
## gato 0.13797317
## león 0.12479193
## corre 0.11994636
## caza 0.13180383
## _ss_ 0.12051845## [,1]
## _s_ 0.03493901
## el 0.04780222
## perro 0.03821035
## gato 0.04690264
## león 0.04308502
## corre 0.33639351
## caza 0.41087194
## _ss_ 0.04179531## [,1]
## _s_ 0.09957218
## el 0.14289131
## perro 0.12246787
## gato 0.13795972
## león 0.12480659
## corre 0.11993921
## caza 0.13183822
## _ss_ 0.12052489## [,1]
## _s_ 0.03489252
## el 0.04769205
## perro 0.03813136
## gato 0.04679205
## león 0.04298749
## corre 0.33663831
## caza 0.41117094
## _ss_ 0.04169529Observación: a partir de este principio, es posible construir arquitecturas más refinadas que tomen en cuenta, por ejemplo, relaciones más lejanas entre partes de oraciones (no solo el contexto del n-grama), ver por ejemplo el capítulo 10 del libro de Deep Learning de Goodfellow, Bengio y Courville.
Abajo exploramos una parte fundamental de estos modelos: representaciones de palabras, y modelos relativamente simples para obtener estas representaciones.
9.2 Representación de palabras
Un aspecto interesante de el modelo de arriba es que nos da una representación vectorial de las palabras, en la forma de los parámetros ajustados de la matriz \(C\). Esta se puede entender como una descripción numérica de cómo funciona una palabra en el contexto de su n-grama.
Por ejemplo, deberíamos encontrar que palabras como “perro” y “gato” tienen representaciones similares. La razón es que cuando aparecen, las probabilidades sobre las palabras siguientes deberían ser similares, pues estas son dos palabras que se pueden usar en muchos contextos compartidos.
También podríamos encontrar que palabras como perro, gato, águila, león, etc. tienen partes o entradas similares en sus vectores de representación, que es la parte que hace que funcionen como “animal mamífero” dentro de frases.
Veremos que hay más razones por las que es interesante esta representación.
9.3 Modelos de word2vec
Si lo que principalmente nos interesa es obtener la representación vectorial de palabras, más recientemente se descubrió que es posible simplificar considerablemente el modelo de arriba para poder entrenarlo mucho más rápido, y obtener una representación que en muchas tareas se desempeña bien ((Mikolov et al. 2013)).
Hay dos ideas básicas que se pueden usar para reducir la complejidad del entrenamiento (ver más en (Goodfellow, Bengio, and Courville 2016) y (Mikolov et al. 2013):
- Eliminar la segunda capa oculta: modelo de bag-of-words continuo y modelo de skip-gram.
- Cambiar la función objetivo (minimizar devianza/maximizar verosimilitud) por una más simple, mediante un truco que se llama negative sampling.
Como ya no es de interés central predecir la siguiente palabra a partir de las anteriores, en estos modelos intentamos predecir la palabra central a partir de las que están alrededor.
9.3.1 Arquitectura continuous bag-of-words
La entrada es igual que en el modelo completo. En primer lugar, simplificamos la segunda capa oculta pondiendo en \(z\) el promedio de los vectores \(C(w_{n-2}), C(w_{n-1})\). La última capa la dejamos igual por el momento:
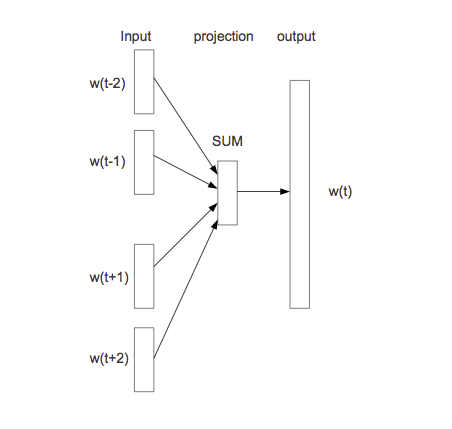
Imagen
El modelo se llama bag-of-words porque todas las entradas de la primera capa oculta contribuyen de la misma manera en la salida, independientemente del orden. Aunque esto no suena como buena idea para construir un modelo de lenguaje, veremos que resulta en una representación adecuada para algunos problemas.
- En la primera capa oculta, tenemos un mapeo de las entradas \(w_1,\ldots, w_{n-1}\) a \(x=C(w_1),\ldots, C(w_{n-1})\), donde \(C\) es una función que mapea palabras a vectores de dimensión \(d\). \(C\) también se puede pensar como una matriz de dimensión \(|V|\) por \(d\). En la capa de entrada,
\[w_{n-2},w_{n-1} \to x = (C(w_{n-2}), C(w_{n-1})).\]
En la siguiente “capa”" oculta simplemente sumamos las entradas de \(x\). Aquí nótese que realmente no hay parámetros.
Finalmente, la capa de salida debe ser un vector de probabilidades sobre todo el vocabulario \(|V|\). En esta capa tenemos pesos \(U\) y hacemos \[y = b + U\sigma (z),\] y finalmente usamos softmax para tener probabilidades que suman uno: \[p_i = \frac{\exp (y_i) }{\sum_j exp(y_j)}.\]
En el ajuste maximizamos la verosimilitud sobre el corpus. Por ejemplo, para una frase, su log verosimilitud es:
\[\sum_t \log \hat{P}(w_{t,n}|w_{t,n+1} \cdots w_{t-n-1}) \]
9.3.2 Arquitectura skip-grams
Otro modelo simplificado, con más complejidad computacional pero mejores resultados (ver (Mikolov et al. 2013)) que el bag-of-words, es el modelo de skip-grams. En este caso, dada cada palabra que encontramos, intentamos predecir un número fijo de las palabras anteriores y palabras posteriores (el contexto es una vecindad de la palabra).
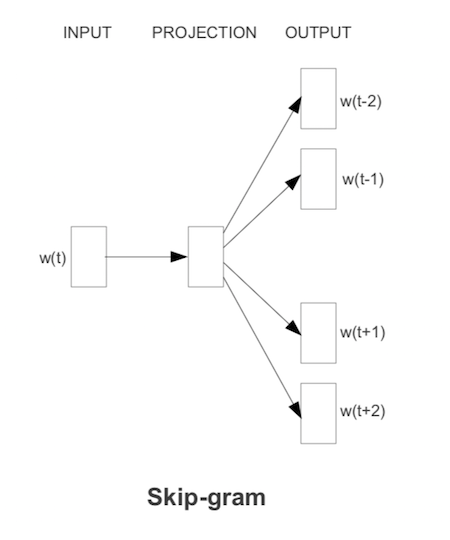
Imagen
La función objetivo se defina ahora (simplificando) como suma sobre \(t\):
\[-\sum_t \sum_{ -2\leq j \leq 2, j\neq 0} \log P(w_{t-j} | w_t)\] (no tomamos en cuenta dónde aparece exactamente \(w_{t-j}\) en relación a \(w_t\), simplemente consideramos que está en su contexto), donde
\[\log P(w_{t-j}|w_t) = u_{t-j}^tC(w_n) - \log\sum_k \exp{u_{k}^tC(w_n)}\]
Todavía se propone una simplificación adicional que resulta ser efectiva:
9.3.3 Muestreo negativo
La siguiente simplificación consiste en cambiar la función objetivo. En word2vec puede usarse “muestreo negativo”.
Para empezar, la función objetivo original (para contexto de una sola palabra) es
\[E = -\log \hat{P}(w_{a}|w_{n}) = -y_{w_a} + \log\sum_j \exp(y_j),\]
donde las \(y_i\) son las salidas de la penúltima capa. La dificultad está en el segundo término, que es sobre todo el vocabulario en incluye todos los parámetros del modelo (hay que calcular las parciales de \(y_j\)’s sobre cada una de las palabras del vocabulario).
La idea del muestreo negativo es que si \(w_a\) está en el contexto de \(w_{n}\), tomamos una muestra de \(k\) palabras \(v_1,\ldots v_k\) al azar (2-50, dependiendo del tamaño de la colección), y creamos \(k\) “contextos falsos” \(v_j w_{n}\), \(j=1\ldots,k\). Minimizamos en lugar de la observación de arriba
\[E = -\log\sigma(y_{w_a}) + \sum_{j=1}^k \log\sigma(y_j),\] en donde queremos maximizar la probabilidad de que ocurra \(w_a\) vs. la probabilidad de que ocurra alguna de las \(v_j\). Es decir, solo buscamos optimizar parámetros para separar lo mejor que podamos la observación de \(k\) observaciones falsas, lo cual implica que tenemos que mover un número relativamente chico de parámetros (en lugar de todos los parámetros de todas las palabras del vocabulario).
Las palabras “falsas” se escogen según una probabilidad ajustada de unigramas (se observó empíricamente mejor desempeño cuando escogemos cada palabra con probabilidad proporcional a \(P(w)^{3/4}\), en lugar de \(P(w)\), ver (Mikolov et al. 2013)).
Ejemplo
library(tidyverse)
periodico <- read_lines(file= "../datos/noticias/Es_Newspapers.txt",
progress = FALSE)
normalizar <- function(texto, vocab = NULL){
# minúsculas
texto <- tolower(texto)
# varios ajustes
texto <- gsub("\\s+", " ", texto)
texto <- gsub("\\.[^0-9]", " _punto_ ", texto)
texto <- gsub(" _s_ $", "", texto)
texto <- gsub("\\.", " _punto_ ", texto)
texto <- gsub("[«»¡!¿?-]", "", texto)
texto <- gsub(";", " _punto_coma_ ", texto)
texto <- gsub("\\:", " _dos_puntos_ ", texto)
texto <- gsub("\\,[^0-9]", " _coma_ ", texto)
texto <- gsub("\\s+", " ", texto)
texto
}
periodico_df <- tibble(txt = periodico) %>%
mutate(id = row_number()) %>%
mutate(txt = normalizar(txt))if(!file.exists('./salidas/noticias_w2v.txt')){
tmp <- tempfile()
# tokenización
write_lines(periodico_df$txt, tmp)
prep <- prep_word2vec(tmp,
destination = './salidas/noticias_w2v.txt', bundle_ngrams = 2)
} Construimos un modelo con vectores de palabras de tamaño 100, skip-grams de tamaño 4, y ajustamos con muestreo negativo de tamaño 20:
if (!file.exists("./salidas/noticias_vectors.bin")) {
model <- train_word2vec("./salidas/noticias_w2v.txt",
"./salidas/noticias_vectors.bin",
vectors = 100, threads = 4, window = 4, cbow = 0,
iter = 5, negative_samples = 20, min_count = 5)
} else {
model <- read.vectors("./salidas/noticias_vectors.bin")
}## total 162M
## drwxr-xr-x 2 rstudio rstudio 4.0K Apr 12 02:15 .
## drwxr-xr-x 24 rstudio rstudio 4.0K May 10 21:48 ..
## -rw-r--r-- 1 rstudio rstudio 0 Dec 21 01:51 .gitignore
## -rw-r--r-- 1 rstudio rstudio 40M Apr 12 02:15 noticias_vectors.bin
## -rw-r--r-- 1 rstudio rstudio 122M Apr 12 01:50 noticias_w2v.txt
## -rw-r--r-- 1 rstudio rstudio 31K May 10 21:30 reglas.csvEl resultado son los vectores aprendidos de las palabras, por ejemplo
## [1] 0.446756899 -0.899206102 -0.345887333 -0.073625632 -0.071392849
## [6] 0.328033894 0.159884691 0.931885242 -0.227679655 0.144669488
## [11] -0.058882836 -0.061171278 0.248835355 0.677498758 -0.056353256
## [16] -0.012200648 -0.144549713 0.384516716 0.705745280 0.679059327
## [21] 0.079138570 0.083563961 0.250697941 0.167539686 0.065761231
## [26] 0.064161301 0.089391224 0.090405807 -0.049623188 -0.172816932
## [31] 0.202728122 0.107696541 -0.139770135 0.033374168 0.457716197
## [36] 0.022019783 0.354458481 0.023252925 0.387462407 -0.539933562
## [41] -0.280268282 0.415804565 -0.041511972 -0.077112705 -0.261035591
## [46] 0.484892517 -0.509083629 0.002850574 0.320239842 0.048141278
## [51] 0.078642599 0.072875679 -0.310345858 0.296670109 -0.067616813
## [56] -0.015224514 0.388360202 0.250751644 -0.443723500 -0.534110487
## [61] -0.815027058 0.202539325 0.366088033 -0.119423777 -0.176932856
## [66] 0.151169926 0.255729765 0.523413181 0.165986717 0.903739989
## [71] 0.265891254 0.138047621 -0.235954061 0.491138607 0.016235521
## [76] 0.099921443 -0.457073390 -0.159864575 0.441086352 0.135879979
## [81] -0.151510969 0.709042013 0.398042202 -0.323476523 0.712096512
## [86] 0.404775172 0.146415085 0.291092187 0.869002044 0.562284470
## [91] 0.199719667 -0.164385915 -0.053073395 -0.127982259 -0.071940482
## [96] 0.487574816 0.153918982 -0.299959272 -0.695077717 -0.1643530289.4 Espacio de representación de palabras
Como discutimos arriba, palabras que se usan en contextos similares por su significado o por su función (por ejemplo, “perro” y “gato”") deben tener representaciones similares, pues su contexto tiende a ser similar. La distancia que usamos el similitud coseno.
Podemos verificar con nuestro ejemplo:
## word similarity to "gol"
## 1 gol 1.0000000
## 2 golazo 0.8129183
## 3 segundo_gol 0.7748883
## 4 doble_penalti 0.7661409
## 5 penalti 0.7595626## word similarity to "presidente"
## 1 presidente 1.0000000
## 2 vicepresidente 0.8512745
## 3 ex_presidente 0.8142816
## 4 secretario_general 0.7517679
## 5 expresidente 0.7256730También podemos buscar varias palabras:
## word similarity to palabras
## 1 nuboso 0.8209098
## 2 nuboso_inicialmente 0.8076709
## 3 soleado 0.8072524
## 4 oeste_moderado 0.7836321
## 5 cierzo_moderado 0.7784690
## 6 lluvioso 0.7767380
## 7 nordeste_flojo 0.7717186
## 8 nieblas_matinales 0.7716210
## 9 intervalos_moderados 0.7709335
## 10 cielo_nuboso 0.7689332Que es lo mismo que:
# extraer vectores de palabras y promediar
vectores <- map(palabras, ~ model[[.x]]) %>%
map(as.numeric) %>% bind_cols
media <- apply(as.matrix(vectores), 1, mean)
model %>% closest_to(t(media))## word similarity to t(media)
## 1 nuboso 0.8209098
## 2 nuboso_inicialmente 0.8076709
## 3 soleado 0.8072524
## 4 oeste_moderado 0.7836321
## 5 cierzo_moderado 0.7784690
## 6 lluvioso 0.7767380
## 7 nordeste_flojo 0.7717186
## 8 nieblas_matinales 0.7716210
## 9 intervalos_moderados 0.7709335
## 10 cielo_nuboso 0.7689332Podemos ver cómo se ven las palabras más similares a “lluvia” o “sol”,
library(ggrepel)
vectores = model[[c("lluvia", "sol"),
average = F]]
sims <- model[1:5000,] %>% # las 5000 palabras más comunes
cosineSimilarity(vectores) %>%
as.data.frame() %>%
rownames_to_column()
similares <- sims %>% filter_at(vars(-rowname), any_vars(. > 0.6))
ggplot(similares, aes(x = lluvia, y = sol, label = rowname)) +
geom_text_repel() + ylab("Similitud con sol") +
xlab("Similitud con lluvia")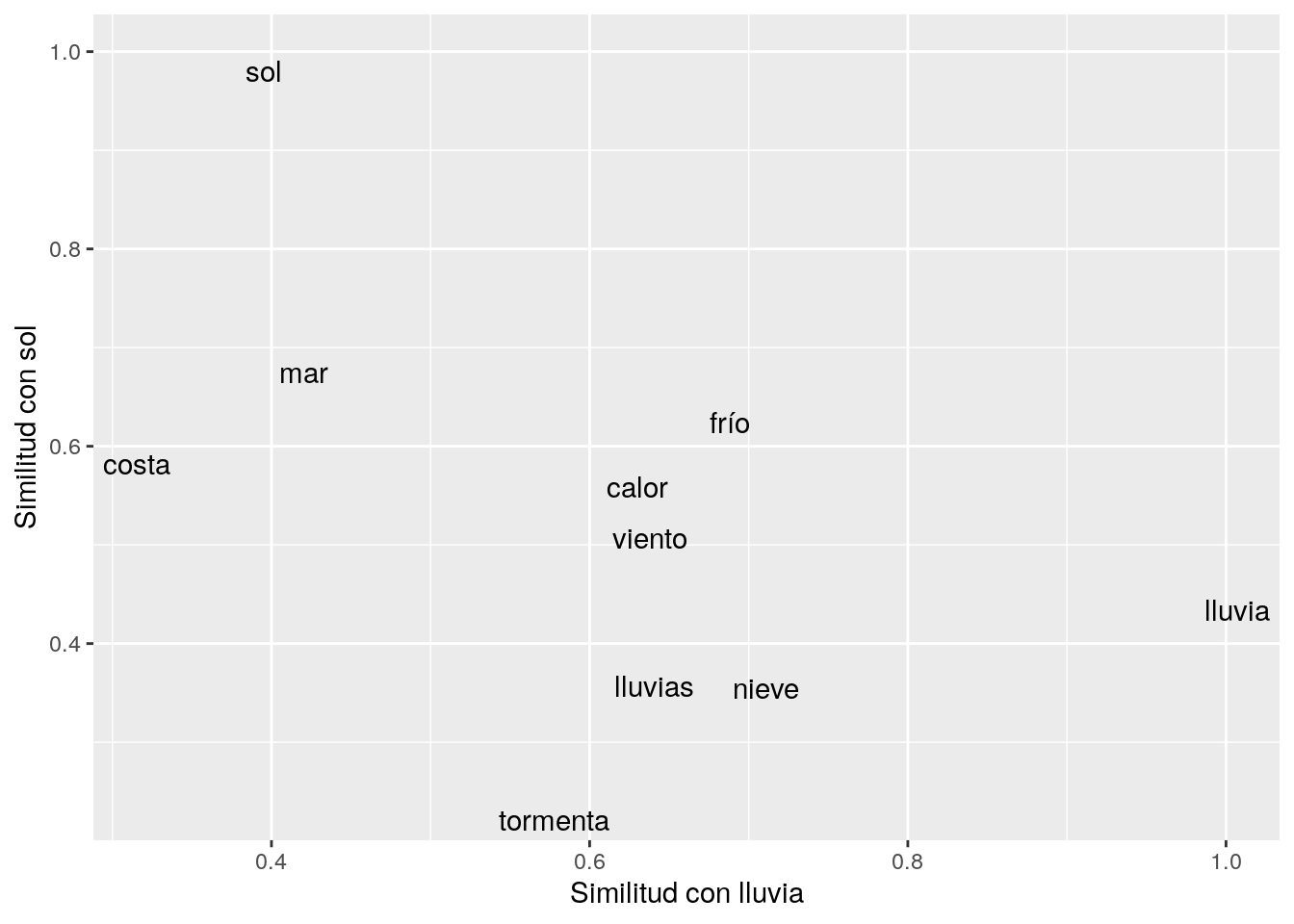
Ahora consideremos cómo se distribuyen las palabras en este espacio, y si existe estructura geométrica en este espacio.
Consideremos primero el caso de plurales de sustantivos.
- Como el contexto de los plurales es distinto de los singulares, nuestro modelo puede capturar en los vectores su diferencia.
- Examinamos entonces cómo son geométricamente diferentes las representaciones de plurales vs singulares
- Si encontramos un patrón reconocible, podemos utilizar este patrón, por ejemplo, para encontrar la versión plural de una palabra singular, sin usar ninguna regla del lenguaje.
Una de las relaciones geométricas más simples es la adición de vectores. Por ejemplo, extraemos la diferencia entre gol y goles:
## A VectorSpaceModel object of 1 words and 100 vectors
## [,1] [,2] [,3] [,4] [,5] [,6]
## [1,] 0.121807 0.4495858 0.1844992 0.06206211 0.5105831 0.4555009
## attr(,".cache")
## <environment: 0x559885459d90>que es un vector en el espacio de representación de palabras. Ahora sumamos este vector a un sustantivo en singular, y vemos qué palabras están cercas de esta “palabra sintética”:
## word similarity to vector
## 1 partidos 0.7775291
## 2 goles 0.7335402
## 3 últimos_encuentros 0.6987743
## 4 encuentros_ligueros 0.6805780
## 5 encuentros 0.6756701Nótese que la más cercana es justamente el plural correcto, o otros plurales con relación al que buscábamos (como encuentros)
Otro ejemplo:
plural_1 <- model[["días"]] - model[["día"]]
vector <- model[["mes"]] + plural_1
model %>% closest_to(vector, n = 20) ## word similarity to vector
## 1 días 0.7639464
## 2 meses 0.7605368
## 3 tres_meses 0.7484373
## 4 seis_meses 0.7208005
## 5 doce_meses 0.7057181
## 6 nueve_meses 0.7009832
## 7 diez_días 0.6801843
## 8 mes 0.6788827
## 9 diez_años 0.6746576
## 10 nueves_meses 0.6680301
## 11 quince_días 0.6502358
## 12 dos_semanas 0.6409786
## 13 años 0.6367727
## 14 quince_años 0.6272623
## 15 semanas 0.6251908
## 16 períodos 0.6227449
## 17 treinta_años 0.6115733
## 18 48_horas 0.6051202
## 19 veinte_años 0.5997798
## 20 25_años 0.5986336Veremos ahora cómo funciona para el género de sustantivos:
fem_1 <- model[["presidenta"]] - model[["presidente"]]
vector <- model[["rey"]] + fem_1
model %>% closest_to(vector, n = 5) %>% filter(word != "rey")## word similarity to vector
## 1 virgen 0.6340726
## 2 princesa 0.6268177
## 3 mismísima 0.6215677
## 4 reina 0.6207278## word similarity to vector
## 1 tía 0.6754675
## 2 bisabuela 0.6544989
## 3 suegra 0.6467780
## 4 madre 0.6456372Y la relación adverbio - adjetivo también podemos considerarla:
adv <- model[["lentamente"]] - model[["lento"]]
vector <- model[["rápido"]] + adv
model %>% closest_to(vector, n = 10) %>% filter(word != "lentamente")## word similarity to vector
## 1 rápidamente 0.6120862
## 2 despacito 0.5945271
## 3 mis_ojos 0.5921103
## 4 deprisa 0.5786580
## 5 unas_copas 0.5771113
## 6 atropelladamente 0.5590286
## 7 luego 0.5587256
## 8 rápido 0.5575443
## 9 abrigado 0.5534166La evaluación de estas aplicaciones puede hacerse por ejemplo, con una lista de singular/plurales, de adjetivos/adverbios, masculino/femenino, etc (ver (Mikolov et al. 2013)).
Observación: falta afinar los parámetros en este modelo. Puedes probar cambiando negative sampling (por ejemplo, incrementa a 40), el número de vectores (50-200, por ejemplo), e incrementando window y el número de iteraciones.
Considera también un modelo preentrenado mucho más grande como este y repite las tareas mostradas (el formato bin es estándar para la implementación que usamos de word2vec).
Podemos visualizar el espacio de representaciones reduciendo dimensionalidad. En este caso, utilizamos tsne:
library(tsne)
library(ggplot2)
library(ggrepel)
mat_vs <- model@.Data
# solo calculamos para las 500 palabras más comunes
num_palabras <- 500
set.seed(1203)
vs_2 <- tsne(mat_vs[1:num_palabras, ],
max_iter = 1000, perplexity = 50)## sigma summary: Min. : 0.535365725279361 |1st Qu. : 0.659265086100002 |Median : 0.746122938806644 |Mean : 0.765409270714441 |3rd Qu. : 0.852518611441111 |Max. : 1.15635147984677 |## Epoch: Iteration #100 error is: 17.8950131944995## Epoch: Iteration #200 error is: 0.808830619283153## Epoch: Iteration #300 error is: 0.771295190301372## Epoch: Iteration #400 error is: 0.762259948196155## Epoch: Iteration #500 error is: 0.758257160347652## Epoch: Iteration #600 error is: 0.756487834813929## Epoch: Iteration #700 error is: 0.755516689488273## Epoch: Iteration #800 error is: 0.755357080064267## Epoch: Iteration #900 error is: 0.755354288780215## Epoch: Iteration #1000 error is: 0.755353631925529set.seed(823)
colnames(vs_2) <- c("V1", "V2")
df_vs <- as_tibble(vs_2, .name_repair = "check_unique") %>%
mutate(palabra = rownames(mat_vs[1:num_palabras, ]))
ggplot(df_vs %>% sample_n(250),
aes(x = V1, y = V2, label = palabra)) +
geom_point(colour = 'red', alpha = 0.3) +
geom_text_repel(size = 2, force = 0.3, segment.alpha = 0.5) 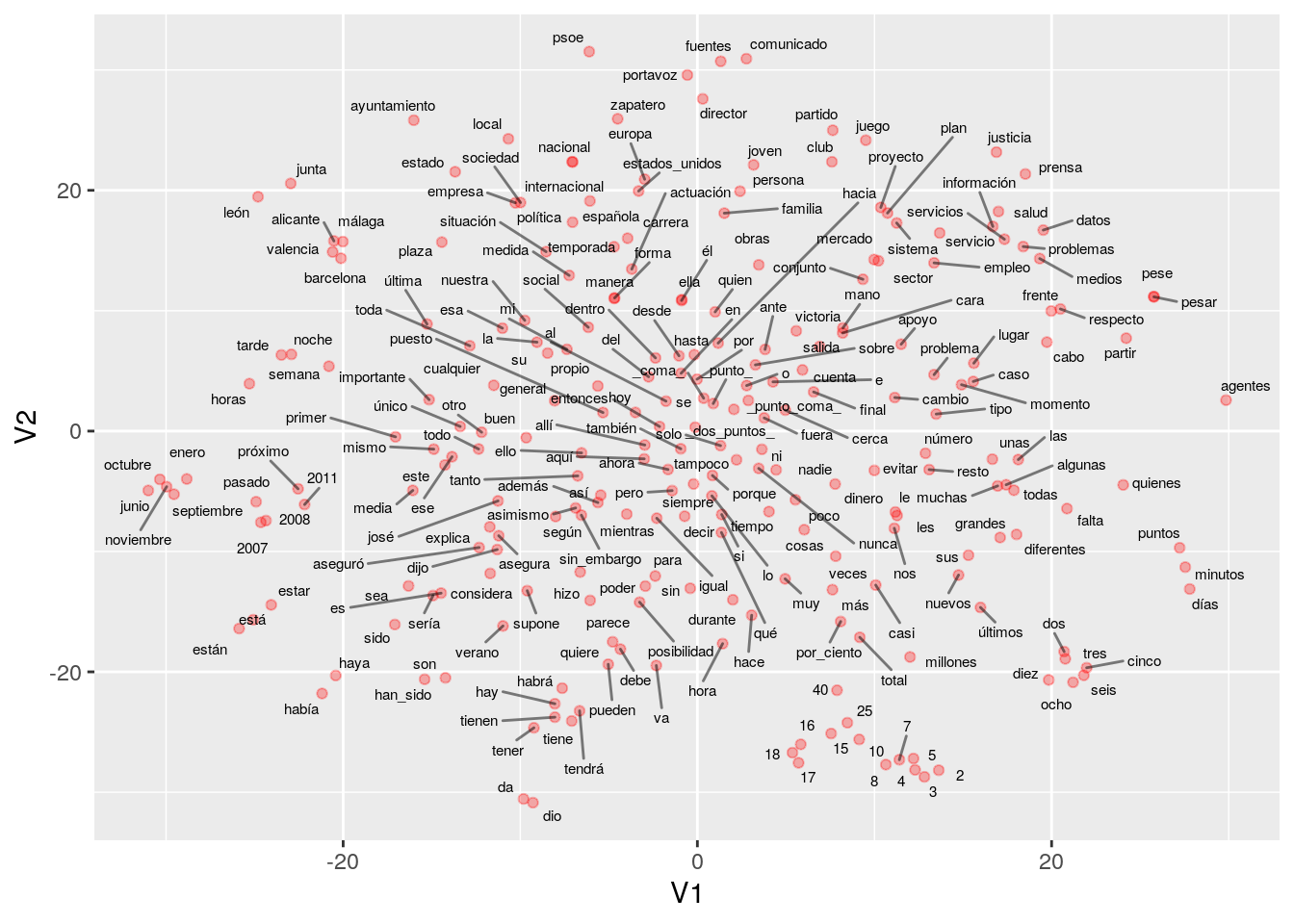
9.5 Usos de representaciones distribuidas
La idea general de construir representaciones densas de las palabras (en lugar de representaciones ralas, como codificación dummy o one-hot encoding) es una fundamental en varias tareas de procesamiento de lenguaje natural. Se utiliza en clasificación de textos (fast-text es similar al modelo bag-of-words), respuesta de preguntas, traducción automática, recuperación de información, reconocimiento de entidades, etc. Word2vec también es usado para sistemas de recomendación (las palabras son artículos, las canastas son los textos).
Referencias
Bengio, Yoshua, Réjean Ducharme, Pascal Vincent, and Christian Janvin. 2003. “A Neural Probabilistic Language Model.” J. Mach. Learn. Res. 3 (March). JMLR.org: 1137–55. http://dl.acm.org/citation.cfm?id=944919.944966.
Goodfellow, Ian, Yoshua Bengio, and Aaron Courville. 2016. Deep Learning. MIT Press.
Mikolov, Tomas, Kai Chen, Greg Corrado, and Jeffrey Dean. 2013. “Efficient Estimation of Word Representations in Vector Space.” CoRR abs/1301.3781. http://arxiv.org/abs/1301.3781.