5 Sistemas de recomendación y filtrado colaborativo
En esta sección discutiremos métodos que se pueden utilizar para hacer recomendaciones de documentos, películas, artículos, etc. a personas según sus intereses.
- Problema: predecir la respuesta de personas a estímulos a los que no han sido expuestos, basados en respuesta a otros estímulos de esta y quizá otras personas similares.
Por ejemplo, si consideramos usuarios de Netflix: ¿qué tanto le puede gustar a X la película Y? Usuarios de Amazon: ¿qué tan probable es que compren Z artículo si se les ofrece?
5.1 Enfoques de recomendación
Hay varios enfoques que podemos utilizar para atacar este problema:
- Principalmente basados en contenido: En función de características de los estímulos, productos o películas (por ejemplo, género, actores, país de origen, año, etc.) intentamos predecir el gusto por el estímulo. En este enfoque, construimos variables derivadas del contenido de los artículos (por ejemplo: qué actores salen, año, etc. o en textos palabras que aparecen), e intentamos predecir el gusto a partir de esas características.
Ejemplo: Si mu gustó Twilight entonces el sistema recomienda otros dramas+vampiros (" por ejemplo “Entrevista con un vampiro”).
- Principalmente colaborativos: utilizamos gustos o intereses de usuarios/artículos similares — en el sentido de que les han gustado los mismos artículos/les gustaron a las mismas personas.
Ejemplo: Me gustó StarWars y Harry Potter, varios otros usuarios a los que también les gustaron estas dos películas también les gustó “Señor de los anillos”, así que recomendamos “Señor de los Anillos”. Entre estos métodos, veremos principalmente métodos basados en reducción de dimensionalidad o modelos de factores latentes: encontrar factores latentes que describan usuarios y películas, y predecimos dependiendo de los niveles de factores latentes de personas y películas.
5.2 Datos
Los datos utilizados para este tipo de sistemas son de dos tipos:
Ratings explícitos dados por los usuarios (por ejemplo, Netflix mucho tiempo fue así: \(1-5\) estrellas)
Ratings implícitos que se derivan de la actividad de los usuarios (por ejemplo, vio la película completa, dio click en la descripción de un producto, etc.).
Ejemplo
Consideramos evaluaciones en escala de gusto: por ejemplo \(1-5\) estrellas, o \(1\)-me disgustó mucho, \(5\)-me gustó mucho, etc.
Podemos representar las evaluaciones como una matriz:
| SWars1 | SWars4 | SWars5 | HPotter1 | HPotter2 | Twilight | |
|---|---|---|---|---|---|---|
| a | 3 | 5 | 5 | 2 | - | - |
| b | 3 | - | 4 | - | - | - |
| c | - | - | - | 5 | 4 | - |
| d | 1 | - | 2 | - | 5 | 4 |
Y lo que queremos hacer es predecir los valores faltantes de esta matriz, y seleccionar para cada usuario los artículos con predicción más alta, por ejemplo
| SWars1 | SWars4 | SWars5 | HPotter1 | HPotter2 | Twilight | |
|---|---|---|---|---|---|---|
| a | 3 | 5 | 5 | 2 | 1.7 | 4.8 |
| b | 3 | 1.9 | 4 | 2.6 | 1.6 | 3.3 |
| c | 2.3 | 1.7 | 3.9 | 5 | 4 | 4.2 |
| d | 1 | 1.9 | 2 | 1.2 | 5 | 4 |
Podemos pensar en este problema como uno de imputación de datos faltantes. Las dificultades particulares de este problema son:
- Datos ralos: cada usuario sólo ha visto y calificado una proporción baja de películas, y hay películas con pocas vistas.
- Escalabilidad: el número de películas y usuarios es generalmente grande
Por estas razones, típicamente no es posible usar técnicas estadísticas de imputación de datos (como imputación estocástica basada en regresión)
- Usaremos mejor métodos más simples basados en similitud entre usuarios y películas y descomposición de matrices.
5.3 Modelos de referencia y evaluación
Vamos a comenzar considerando modelos muy simples. El primero que se nos puede ocurrir es uno de homogeneidad de gustos: para una persona \(i\), nuestra predicción de su gusto por la película \(j\) es simplemente la media de la película \(j\) sobre todos los usuarios que la han visto.
Este sería un buen modelo si los gustos fueran muy parecidos sobre todos los usuarios. Esta sería una recomendación de “artículos populares”.
Introducimos la siguente notación:
- \(x_{ij}\) es la evaluación del usuario \(i\) de la película \(j\). Obsérvese que muchos de estos valores no son observados (no tenemos información de varias \(x_{ij}\)).
- \(\hat{x}_{ij}\) es la predicción que hacemos de gusto del usuario \(i\) por la película \(j\)
En nuestro primer modelo simple, nuestra predicción es simplemente \[\hat{x}_{ij} = \hat{b}_j\] donde \[\hat{b_j} = \frac{1}{N_j}\sum_{s} x_{sj},\] y este promedio es sobre los \(N_j\) usuarios que vieron (y calificaron) la película \(j\).
¿Cómo evaluamos nuestras predicciones?
5.3.1 Evaluación de predicciones
Usamos muestras de entrenamiento y validación. Como en el concurso de Netflix, utilizaremos la raíz del error cuadrático medio:
\[RECM =\left ( \frac{1}{T} \sum_{(i,j) \, observada} (x_{ij}-\hat{x}_{ij})^2 \right)^{\frac{1}{2}}\]
aunque también podríamos utilizar la desviación absoluta media:
\[DAM =\frac{1}{T} \sum_{(i,j) \, observada} |x_{ij}-\hat{x}_{ij}|\]
- Nótese que estas dos cantidades se evaluán sólo sobre los pares \((i,j)\) para los que tengamos una observación \(x_{ij}\).
Observaciones:
Generalmente evaluamos sobre un conjunto de validación separado del conjunto de entrenamiento.
Escogemos una muestra de películas, una muestra de usuarios, y ponemos en validación el conjunto de calificaciones de esos usuarios para esas películas.
Para hacer un conjunto de prueba, idealmente los datos deben ser de películas que hayan sido observadas por los usuarios en el futuro (después del periodo de los datos de entrenamiento).
Nótese que no seleccionamos todas las evaluaciones de un usuario, ni todas las evaluaciones de una película. Con estas estrategias, veríamos qué pasa con nuestro modelo cuando tenemos una película que no se ha visto o un usuario nuevo. Lo que queremos ententer es cómo se desempeña nuestro sistema cuando tenemos cierta información de usuarios y de películas.
Ejemplo: datos de Netflix
Los datos del concurso de Netflix originalmente vienen en archivos de texto, un archivo por película.
The movie rating files contain over \(100\) million ratings from \(480\) thousand randomly-chosen, anonymous Netflix customers over \(17\) thousand movie titles. The data were collected between October, \(1998\) and December, \(2005\) and reflect the distribution of all ratings received during this period. The ratings are on a scale from \(1\) to \(5\) (integral) stars. To protect customer privacy, each customer id has been replaced with a randomly-assigned id. The date of each rating and the title and year of release for each movie id are also provided.
The file “training_set.tar” is a tar of a directory containing \(17770\) files, one per movie. The first line of each file contains the movie id followed by a colon. Each subsequent line in the file corresponds to a rating from a customer and its date in the following format:
CustomerID,Rating,Date
- MovieIDs range from \(1\) to \(17770\) sequentially.
- CustomerIDs range from \(1\) to \(2649429\), with gaps. There are \(480189\) users.
- Ratings are on a five star (integral) scale from \(1\) to \(5\).
- Dates have the format YYYY-MM-DD.
En primer lugar haremos un análisis exploratorio de los datos para entender algunas de sus características, ajustamos el modelo simple de gustos homogéneos (la predicción es el promedio de calificaciones de cada película), y lo evaluamos.
Comenzamos por cargar los datos:
library(tidyverse)
library(sparklyr)
theme_set(theme_minimal())
cb_palette <- c("#000000", "#E69F00", "#56B4E9", "#009E73", "#F0E442", "#0072B2", "#D55E00", "#CC79A7")## Parsed with column specification:
## cols(
## X1 = col_double(),
## X2 = col_double(),
## X3 = col_character()
## )names(pelis_nombres) <- c('peli_id','año','nombre')
dat_netflix <- read_csv( "../datos/netflix/dat_muestra_nflix.csv", progress = FALSE) %>%
select(-usuario_id_orig) %>%
mutate(usuario_id = as.integer(as.factor(usuario_id)))## Parsed with column specification:
## cols(
## peli_id = col_double(),
## usuario_id_orig = col_double(),
## calif = col_double(),
## fecha = col_date(format = ""),
## usuario_id = col_double()
## )## # A tibble: 6 x 4
## peli_id calif fecha usuario_id
## <dbl> <dbl> <date> <int>
## 1 1 3 2004-04-14 1
## 2 1 3 2004-12-28 2
## 3 1 4 2004-04-06 3
## 4 1 4 2004-03-07 4
## 5 1 4 2004-03-29 5
## 6 1 2 2004-07-11 6## # A tibble: 1 x 1
## n
## <int>
## 1 20968941Y ahora calculamos las medias de cada película.
medias_pelis <- dat_netflix %>% group_by(peli_id) %>%
summarise(media_peli = mean(calif), num_calif_peli = n())
medias_pelis <- left_join(medias_pelis, pelis_nombres)## Joining, by = "peli_id"arrange(medias_pelis, desc(media_peli)) %>%
top_n(200, media_peli) %>%
mutate(media_peli = round(media_peli, 2)) %>%
DT::datatable()Nótese que varias de las películas con mejor promedio tienen muy pocas evaluaciones. Podemos examinar más detalladamente graficando número de evaluaciones vs promedio:
ggplot(medias_pelis, aes(x=num_calif_peli, y=media_peli)) +
geom_point(alpha = 0.1) + xlab("Número de calificaciones") +
ylab("Promedio de calificaciones") 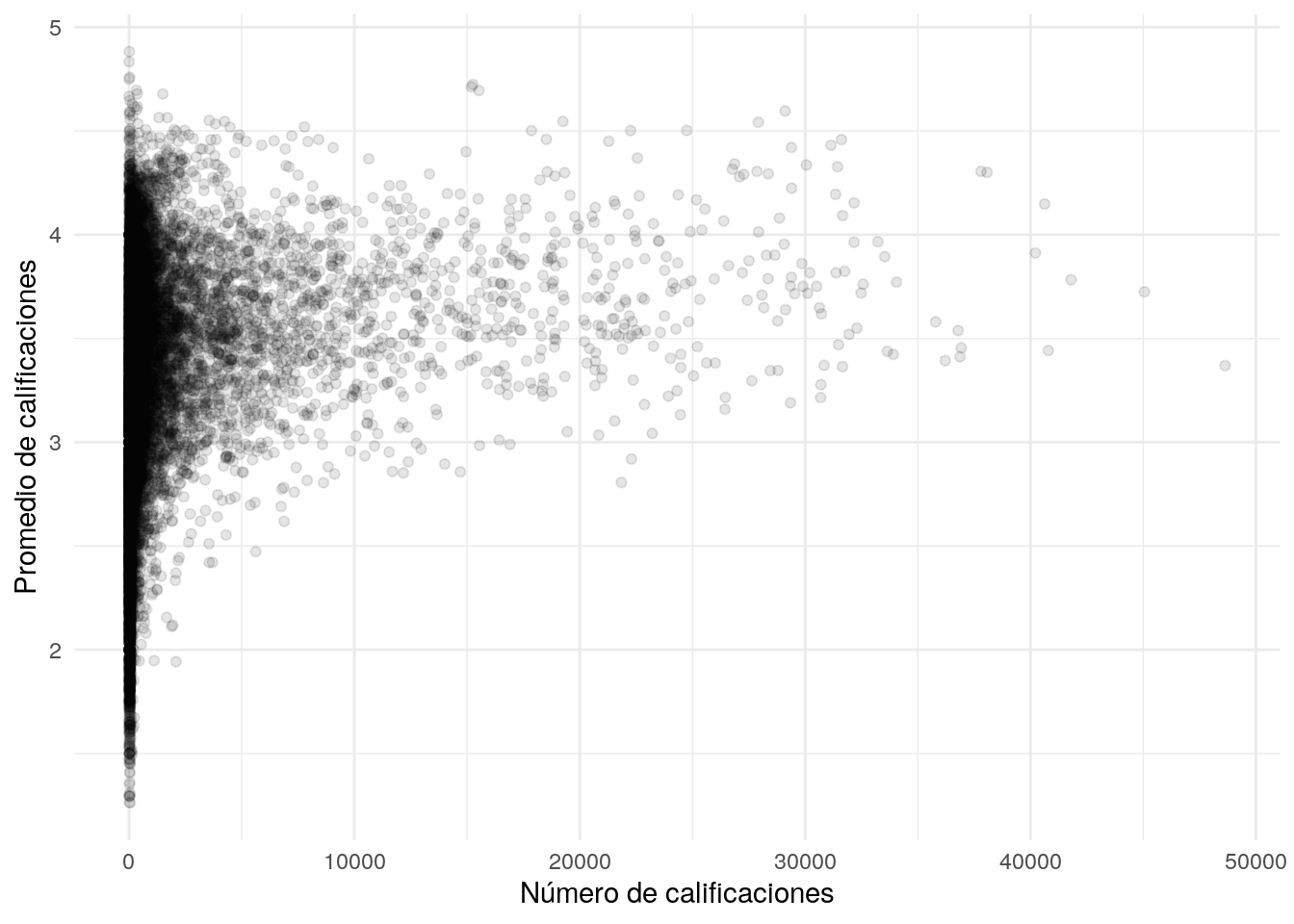
Y vemos que hay más variabilidad en los promedios cuando hay menos evaluaciones, como es de esperarse. ¿Puedes ver algún problema que tendremos que enfrentar con el modelo simple?
Si filtramos por número de calificaciones (al menos \(500\) por ejemplo), estas son las películas mejor calificadas (la mayoría conocidas y populares):
arrange(medias_pelis, desc(media_peli)) %>%
filter(num_calif_peli > 500) %>%
top_n(200, media_peli) %>%
mutate(media_peli = round(media_peli, 2)) %>%
DT::datatable()Ahora seleccionamos nuestra muestra de entrenamiento y de validación. Seleccionamos una muestra de usuarios y de películas:
set.seed(28882)
usuarios <- dat_netflix %>% select(usuario_id) %>% distinct
valida_usuarios <- usuarios %>% sample_frac(0.2)
peliculas <- dat_netflix %>% select(peli_id) %>% distinct
valida_pelis <- peliculas %>% sample_frac(0.2)Y separamos calificaciones de entrenamiento y validación:
## Joining, by = "usuario_id"Joining, by = "peli_id"## Joining, by = c("peli_id", "calif", "fecha", "usuario_id")n_valida <- dat_valida %>% tally %>% pull(n)
n_entrena <- dat_entrena %>% tally %>% pull(n)
sprintf("Entrenamiento: %1d, Validación: %2d, Total: %3d", n_entrena,
n_valida, n_entrena + n_valida)## [1] "Entrenamiento: 20191991, Validación: 776950, Total: 20968941"Ahora construimos predicciones con el modelo simple de arriba y evaluamos con validación:
medias_pred <- dat_entrena %>% group_by(peli_id) %>%
summarise(media_pred = mean(calif))
media_total_e <- dat_entrena %>% ungroup %>% summarise(media = mean(calif)) %>% pull(media)
dat_valida_pred <- dat_valida %>% left_join(medias_pred %>% collect())
head(dat_valida_pred)## # A tibble: 6 x 5
## peli_id calif fecha usuario_id media_pred
## <dbl> <dbl> <date> <int> <dbl>
## 1 2 5 2005-07-18 116 3.64
## 2 2 4 2005-06-07 126 3.64
## 3 2 4 2005-07-30 129 3.64
## 4 2 1 2005-09-07 131 3.64
## 5 2 1 2005-02-13 103 3.64
## 6 8 1 2005-03-21 1007 3.19Nota que puede ser que algunas películas seleccionadas en validación no tengan evaluaciones en entrenamiento:
##
## FALSE
## 776950dat_valida_pred <- mutate(dat_valida_pred,
media_pred = ifelse(is.na(media_pred), media_total_e, media_pred))No sucede en este ejemplo, pero si sucediera podríamos usar el promedio general de las predicciones. Evaluamos ahora el error:
recm <- function(calif, pred){
sqrt(mean((calif - pred)^2))
}
error <- dat_valida_pred %>% ungroup %>%
summarise(error = mean((calif - media_pred)^2))
error## # A tibble: 1 x 1
## error
## <dbl>
## 1 1.03Este error está en las mismas unidades de las calificaciones (estrellas en este caso).
Antes de seguir con nuestra refinación del modelo, veremos algunas observaciones acerca del uso de escala en análisis de datos:
Cuando tratamos con datos en escala encontramos un problema técnico que es el uso distinto de la escala por los usuarios, muchas veces independientemente de sus gustos
Veamos los datos de Netflix para una muestra de usuarios:
# muestra de usuarios
entrena_usu <- sample(unique(dat_entrena$usuario_id), 50)
muestra_graf <- filter(dat_entrena, usuario_id %in% entrena_usu)
# medias generales por usuario, ee de la media
muestra_res <- muestra_graf %>% group_by(usuario_id) %>%
summarise(media_calif = mean(calif),
sd_calif = sd(calif)/sqrt(length(calif)))
muestra_res$usuario_id <- reorder(factor(muestra_res$usuario_id), muestra_res$media_calif)
ggplot(muestra_res, aes(x=factor(usuario_id), y = media_calif,
ymin = media_calif - sd_calif, ymax = media_calif + sd_calif)) +
geom_linerange() + geom_point() + xlab('Usuario ID') +
theme(axis.text.x=element_blank())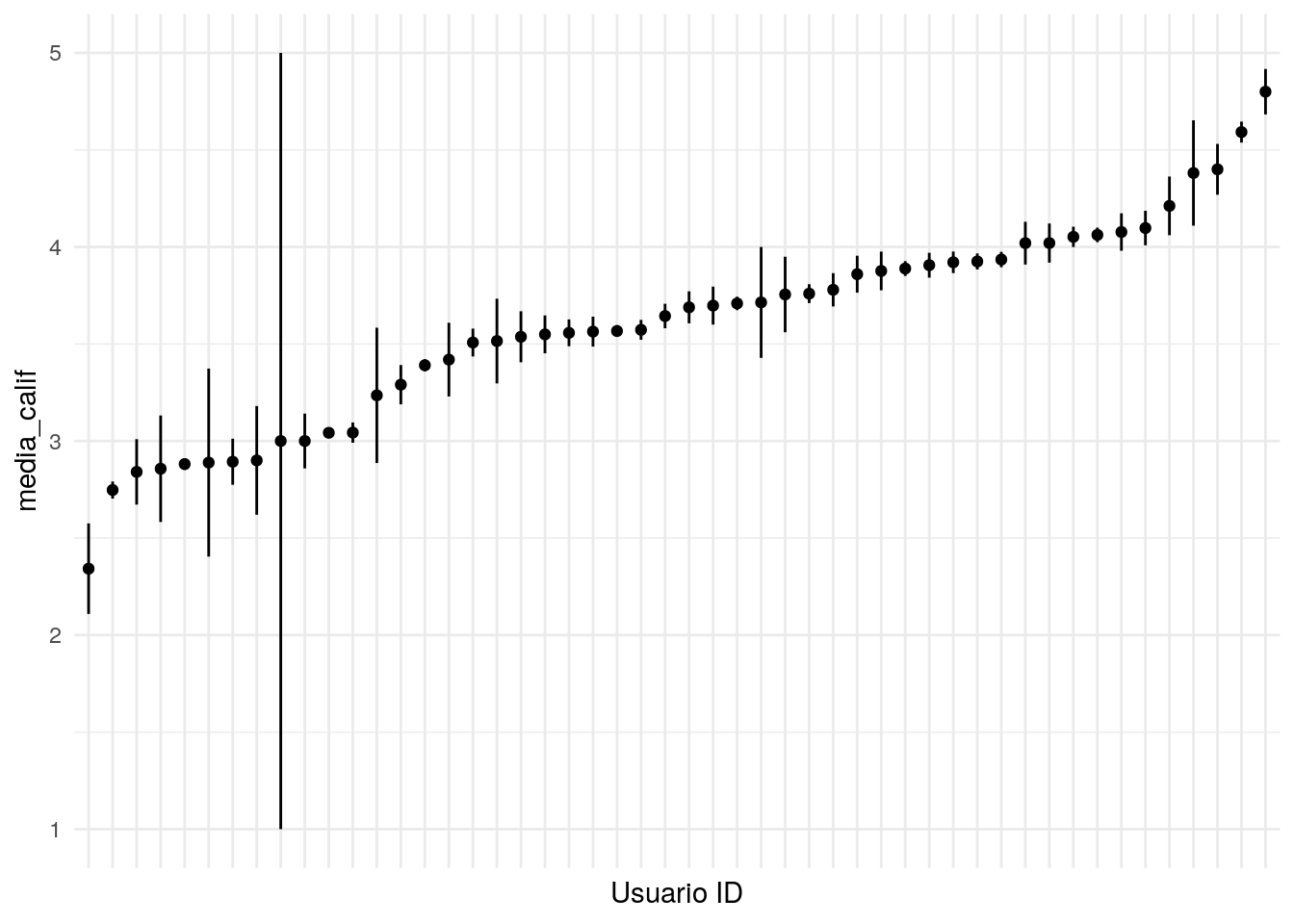
Y notamos que hay unos usuarios que tienen promedios por encima de \(4.5\), mientras que otros califican por debajo de \(3\) en promedio. Aunque esto puede deberse a las películas que han visto, generalmente una componente de esta variabilidad se debe a cómo usa la escala cada usuario.
- En primer lugar, quizá uno podría pensar que un modelo base consiste de simplemente predecir el promedio de una película sobre todos los usuarios que la calificaron (sin incluir el sesgo de cada persona). Esto no funciona bien porque típicamente hay distintos patrones de uso de la escala de calificación, que depende más de forma de uso de escala que de la calidad de los items.
Hay personas que son:
- Barcos: \(5\),\(5\),\(5\),\(4\),\(4\),\(5\)
- Estrictos: \(2\),\(3\),\(3\),\(1\),\(1\),\(2\)
- No se compromete: \(3\),\(3\),\(3\),\(3\),\(4\)
- Discrimina: \(5\),\(4\),\(5\),\(1\),\(2\),\(4\)
El estilo de uso de las escalas varía por persona. Puede estar asociado a aspectos culturales (países diferentes usan escalas de manera diferente), quizá también de personalidad, y a la forma de obtener las evaluaciones (cara a cara, por teléfono, internet).
Lo primero que vamos a hacer para controlar esta fuente de variación es ajustar las predicciones dependiendo del promedio de calificaciones de cada usuario.
5.3.2 (Opcional) Efectos en análisis de heterogeneidad en uso de escala
Muchas veces se considera que tratar como numéricos a calificaciones en escala no es muy apropiado, y que el análisis no tiene por qué funcionar pues en realidad las calificaciones están en una escala ordinal. Sin embargo,
La razón principal por las que análisis de datos en escala es difícil no es que usemos valores numéricos para los puntos de la escala. Si esto fuera cierto, entonces por ejemplo, transformar una variable con logaritmo también sería “malo”.
La razón de la dificultad es que generalmente tenemos que lidiar con la heterogeneidad en uso de la escala antes de poder obtener resultados útiles de nuestro análisis.
Supongamos que \(X_1\) y \(X_2\) son evaluaciones de dos películas. Por la discusión de arriba, podríamos escribir
\[X_1 = N +S_1,\] \[X_2 = N + S_2,\]
donde \(S_1\) y \(S_2\) representan el gusto por la película, y \(N\) representa el nivel general de calificaciones. Consideramos que son variables aleatorias (\(N\) varía con las personas, igual que \(S_1\) y \(S_2\)).
Podemos calcular
\[Cov(X_1,X_2)\]
para estimar el grado de correlación de gusto por las dos películas, como si fueran variables numéricas. Esta no es muy buena idea, pero no tanto porque se trate de variables ordinales, sino porque en realidad quisiéramos calcular:
\[Cov(S_1, S_2)\]
que realmente representa la asociación entre el gusto por las dos películas. El problema es que \(S_1\) y \(S_2\) son variables que no observamos.
¿Cómo se relacionan estas dos covarianzas?
\[Cov(X_1,X_2)=Cov(N,N) + Cov(S_1,S_2) + Cov(N, S_2)+Cov(N,S_1)\]
Tenemos que \(Cov(N,N)=Var(N)=\sigma_N ^2\), y suponiendo que el gusto no está correlacionado con los niveles generales de respuesta, \(Cov(N_1, S_2)=0=Cov(N_2,S_1)\), de modo que
\[Cov(X_1,X_2)= Cov(S_1,S_2) + \sigma_N^2.\]
donde \(\sigma_N^2\) no tiene qué ver nada con el gusto por las películas.
De forma que al usar estimaciones de \(Cov(X_1,X_2)\) para estimar \(Cov(S_1,S_2)\) puede ser mala idea porque el sesgo hacia arriba puede ser alto, especialmente si la gente varía mucho es un sus niveles generales de calificaciones (hay muy barcos y muy estrictos).
5.3.3 Ejemplo
Los niveles generales de \(50\) personas:
## Warning: `data_frame()` is deprecated, use `tibble()`.
## This warning is displayed once per session.Ahora generamos los gustos (latentes) por dos artículos, que suponemos con correlación negativa:
x <- rnorm(n)
gustos <- data.frame(persona=1:n, gusto_1 = x + rnorm(n),
gusto_2 = -x + rnorm(n))
head(gustos,3)## persona gusto_1 gusto_2
## 1 1 0.9478878 0.4586253
## 2 2 1.1499476 -0.6762914
## 3 3 -1.3092422 2.5849039## gusto_1 gusto_2
## gusto_1 1.0000000 -0.5136434
## gusto_2 -0.5136434 1.0000000Estos dos items tienen gusto correlacionado negativamente:
## `geom_smooth()` using method = 'loess' and formula 'y ~ x'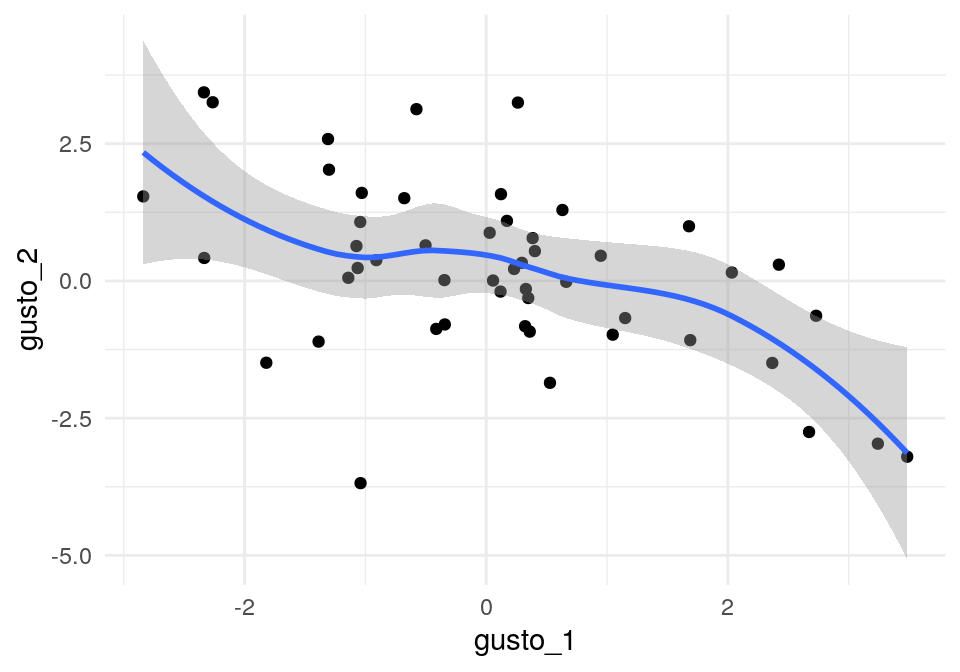
Pero las mediciones no están correlacionadas:
medicion_1 <- niveles$nivel + gustos$gusto_1+rnorm(n,0.3)
medicion_2 <- niveles$nivel + gustos$gusto_2+rnorm(n,0.3)
mediciones <- data_frame(persona = 1:n, medicion_1, medicion_2)
cor(mediciones[,2:3])## medicion_1 medicion_2
## medicion_1 1.00000000 -0.05825995
## medicion_2 -0.05825995 1.00000000Así que aún cuando el gusto por \(1\) y \(2\) están correlacionadas negativamente, las mediciones de gusto no están correlacionadas.
## `geom_smooth()` using method = 'loess' and formula 'y ~ x'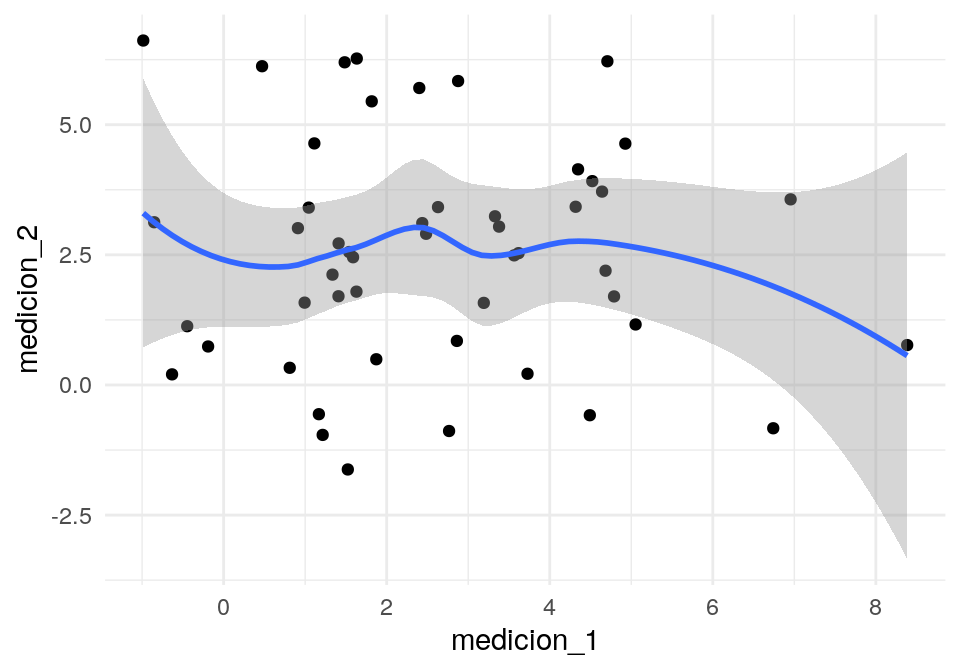
Observaciones: Un modelado más cuidadoso de este tipo de datos requiere más trabajo. Pero para el trabajo usual, generalmente intentamos controlar parte de la heterogeneidad centrando las calificaciones por usuario. Es decir, a cada calificación de una persona le restamos la media de sus calificaciones, que es una estimación del nivel general \(N\). Esta idea funciona si \(k\) no es muy chico.
Si el número de calificaciones por persona (\(k\)) es chico, entonces tenemos los siguientes problemas:
El promedio de evaluaciones es una estimación ruidosa del nivel general.
Podemos terminar con el problema opuesto: nótese que si \(X_1,\ldots, X_k\) son mediciones de gusto distintos items, entonces \[Cov(X_1-\bar{X}, X_2-\bar{X})=Cov(S_1-\bar{S},S_2-\bar{S}),\] \[=Cov(S_1,S_2)-Cov(S_1,\bar{S})-Cov(S_2,\bar{S}) + Var(\bar{S})\]
Si \(k\) es chica, suponiendo que los gustos no están correlacionados, los términos intermedios puede tener valor negativo relativamente grande ( es de orden \(\frac{1}{k}\)), aún cuando el último término sea chico (de orden \(\frac{1}{k^2}\))
Así que ahora las correlaciones estimadas pueden tener sesgo hacia abajo, especialmente si \(k\) es chica.
Más avanzado, enfoque bayesiano: https://www.jstor.org/stable/2670337
5.4 Modelo de referencia
Ahora podemos plantear el modelo base de referencia. Este modelo es útil para hacer benchmarking de intentos de predicción, como primera pieza para construcción de modelos más complejos, y también como una manera simple de producir estimaciones cuando no hay datos suficientes para hacer otro tipo de predicción.
Si \(x_{ij}\) es el gusto del usuario \(i\) por la película \(j\), entonces nuestra predicción es \[\hat{x}_{ij} = \hat{b}_j + (\hat{a}_i-\hat{\mu} ) \]
donde \(a_i\) indica un nivel general de calificaciones del usuario \(i\), y \(b_j\) es el nivel general de gusto por la película.Usualmente ponemos:
- Media general \[\hat{\mu} =\frac{1}{T}\sum_{s,t} x_{st}\]
- Promedio de calificaciones de usuario \(i\) \[\hat{a}_i =\frac{1}{M_i}\sum_{t} x_{i,t} \]
- Promedio de calificaciones de la película \(j\) \[\hat{b}_j =\frac{1}{N_j}\sum_{s} x_{s,j}\]
También podemos escribir, en términos de desviaciones:
\[\hat{x}_{ij} = \hat{\mu} + \hat{c}_i + \hat{d}_j \] donde:
- Media general \[\hat{\mu} =\frac{1}{T}\sum_{s,t} x_{st}\]
- Desviación de las calificaciones de usuario \(i\) respecto a la media general \[\hat{c}_i =\frac{1}{M_i}\sum_{t} x_{it} - \hat{\mu} \]
- Desviación de la película \(j\) respecto a la media general \[\hat{d_j} =\frac{1}{N_j}\sum_{s} x_{sj}- \hat{\mu}\]
Una vez que observamos una calificación \(x_{ij}\), el residual del modelo de referencia es \[r_{ij} = x_{ij} - \hat{x_{ij}}\]
Ejercicio: modelo de referencia para Netflix
Calculamos media de películas, usuarios y total:
medias_usuarios <- dat_entrena %>%
group_by(usuario_id) %>%
summarise(media_usu = mean(calif), num_calif_usu = length(calif)) %>%
select(usuario_id, media_usu, num_calif_usu)
medias_peliculas <- dat_entrena %>%
group_by(peli_id) %>%
summarise(media_peli = mean(calif), num_calif_peli = length(calif)) %>%
select(peli_id, media_peli, num_calif_peli)
media_total_e <- mean(dat_entrena$calif)Y construimos las predicciones para el conjunto de validación
dat_valida <- dat_valida %>%
left_join(medias_usuarios) %>%
left_join(medias_peliculas) %>%
mutate(media_total = media_total_e) %>%
mutate(pred = media_peli + (media_usu - media_total)) %>%
mutate(pred = ifelse(is.na(pred), media_total, pred))## Joining, by = "usuario_id"Joining, by = "peli_id"Nótese que cuando no tenemos predicción bajo este modelo para una combinación de usuario/película, usamos el promedio general (por ejemplo).
Finalmente evaluamos
## # A tibble: 1 x 1
## error
## <dbl>
## 1 0.929Observación: ¿Qué tan bueno es este resultado? De wikipedia:
Prizes were based on improvement over Netflix’s own algorithm, called Cinematch, or the previous year’s score if a team has made improvement beyond a certain threshold. A trivial algorithm that predicts for each movie in the quiz set its average grade from the training data produces an RMSE of \(1.0540\). Cinematch uses “straightforward statistical linear models with a lot of data conditioning”.
Using only the training data, Cinematch scores an RMSE of \(0.9514\) on the quiz data, roughly a 10% improvement over the trivial algorithm. Cinematch has a similar performance on the test set, \(0.9525\). In order to win the grand prize of \(1,000,000\), a participating team had to improve this by another \(10%\), to achieve \(0.8572\) on the test set. Such an improvement on the quiz set corresponds to an RMSE of \(0.8563\).
Aunque nótese que estrictamente hablando no podemos comparar nuestros resultados con estos números, en los que se usa una muestra de prueba separada de películas vistas despúes del periodo de entrenamiento.
Ejercicio: regularización del modelo simple
No hemos resulto el problema de películas o usarios con pocas evaluaciones. Como vimos arriba, hay gran variabilidad en los promedios de las películas con pocas evaluaciones, y esto produce error adicional en nuestras predicciones.
medias_peliculas <- dat_netflix %>% group_by(peli_id) %>% summarise(media_peli = mean(calif), num_calif_peli = length(calif))
media_gral <- mean(dat_netflix$calif)
medias_p_2 <- left_join(medias_peliculas, pelis_nombres)## Joining, by = "peli_id"## # A tibble: 6 x 5
## peli_id media_peli num_calif_peli año nombre
## <dbl> <dbl> <int> <dbl> <chr>
## 1 14791 4.88 17 2003 Trailer Park Boys: Season 3
## 2 8964 4.83 6 2003 Trailer Park Boys: Season 4
## 3 6522 4.76 29 2001 Trailer Park Boys: Seasons 1 & 2
## 4 4614 4.75 4 1964 Blood and Black Lace
## 5 14961 4.72 15260 2003 Lord of the Rings: The Return of the …
## 6 7230 4.71 15191 2001 The Lord of the Rings: The Fellowship…Una opción es encoger calificaciones a la media dependiendo del tamaño de muestra. Por ejemplo:
\[ \hat{x_{ij}} = \hat{\mu} + \frac{n_i}{n_i+\lambda} \hat{c_i} + \frac{m_i}{m_i + \lambda}\hat{d_j} \] Que equivale a encoger las predicciones hacia la media general cuando el número de evaluaciones es bajo. El grado de encogimiento depende de \(\lambda\).
pred_encoger <- function(media, num_usuario, num_peli, media_usu, media_peli, calif, lambda){
coef_usu <- 1 / (1 + lambda / num_usuario)
coef_peli <- 1 / (1 + lambda / num_peli)
pred <- media + coef_usu * (media_usu - media) + coef_peli * (media_peli - media)
pred <- ifelse(is.na(pred), media, pred) # en caso de que no haya califs de usuario o peli
pred
}
lambdas <- c(0.01, 0.1, 1, 5, 10, 20, 100)
error_valida <- map_dfr(lambdas, function(lambda){
preds <- as.tibble(dat_valida) %>%
mutate(pred_lambda = pred_encoger(media_total, num_calif_usu, num_calif_peli,
media_usu, media_peli, calif, lambda)) %>%
select(pred_lambda, calif)
list(lambda = lambda, error = recm(preds$calif, preds$pred_lambda))
})## Warning: `as.tibble()` is deprecated, use `as_tibble()` (but mind the new semantics).
## This warning is displayed once per session.
No logramos una mejora considerable. Veremos más adelante cómo lidiar con este problema de una mejor manera.
5.5 Filtrado colaborativo: similitud
Además de usar promedios generales por película, podemos utilizar similitud de películas/personas para ajustar predicciones según los gustos de artículos o películas similares. Este es el enfoque más simple del filtrado colaborativo.
Comencemos entonces con la siguiente idea: Supongamos que queremos hacer una predicción para el usuario \(i\) en la película \(j\), que no ha visto. Si tenemos una medida de similitud entre películas, podríamos buscar películas similares a \(j\) que haya visto \(i\), y ajustar la predicción según la calificación de estas películas similares.
Tomamos entonces nuestra predicción base, que le llamamos \(x_{ij}^0\) y hacemos una nueva predicción:
\[\hat{x}_{ij} = x_{ij}^0 + \frac{1}{k}\sum_{t \in N(i,j)} (x_{it} - x_{it}^0 )\]
donde \(N(i,j)\) son películas similares a \(j\) que haya visto \(i\). Ajustamos \(x_{ij}^0\) por el gusto promedio de películas similares a \(j\), a partir de las predicciones base. Esto quiere decir que si las películas similares a \(j\) están evaluadas por encima del esperado para el usuario \(i\), entonces subimos la predicción, y bajamos la predicción cuando las películas similares están evaluadas por debajo de lo esperado.
Nótese que estamos ajustando por los residuales del modelo base. Podemos también utilizar un ponderado por gusto según similitud: si la similitud entre las películas \(j\) y \(t\) es \(s_{jt}\), entonces podemos usar
\[\begin{equation} \hat{x}_{ij} = x_{ij}^0 + \frac{\sum_{t \in N(i,j)} s_{jt}(x_{it} - x_{it}^0 )}{\sum_{t \in N(i,j)} s_{jt}} \tag{5.1} \end{equation}\]
Cuando no tenemos películas similares que hayan sido calificadas por nuestro usuario, entonces usamos simplemente la predicción base.
5.5.1 Cálculo de similitud entre usuarios/películas
Proponemos utilizar la distancia coseno de las calificaciones centradas por usuario. Como discutimos arriba, antes de calcular similitud conviene centrar las calificaciones por usuario para eliminar parte de la heterogeneidad en el uso de la escala.
Ejemplo
| SWars1 | SWars4 | SWars5 | HPotter1 | HPotter2 | Twilight | |
|---|---|---|---|---|---|---|
| a | 5 | 5 | 5 | 2 | NA | NA |
| b | 3 | NA | 4 | NA | NA | NA |
| c | NA | NA | NA | 5 | 4 | NA |
| d | 1 | NA | 2 | NA | 5 | 4 |
| e | 4 | 5 | NA | NA | NA | 2 |
Calculamos medias por usuarios y centramos:
## a b c d e
## 4.250000 3.500000 4.500000 3.000000 3.666667| SWars1 | SWars4 | SWars5 | HPotter1 | HPotter2 | Twilight | |
|---|---|---|---|---|---|---|
| a | 0.75 | 0.75 | 0.75 | -2.25 | NA | NA |
| b | -0.50 | NA | 0.50 | NA | NA | NA |
| c | NA | NA | NA | 0.50 | -0.5 | NA |
| d | -2.00 | NA | -1.00 | NA | 2.0 | 1.00 |
| e | 0.33 | 1.33 | NA | NA | NA | -1.67 |
Y calculamos similitud coseno entre películas, suponiendo que las películas no evaluadas tienen calificación \(0\):
sim_cos <- function(x,y){
sum(x*y, na.rm = T)/(sqrt(sum(x^2, na.rm = T))*sqrt(sum(y^2, na.rm = T)))
}
mat.c[,1]## a b c d e
## 0.7500000 -0.5000000 NA -2.0000000 0.3333333## a b c d e
## 0.750000 NA NA NA 1.333333## [1] 0.2966402## [1] -0.5925503Observación:
Hacer este supuesto de valores \(0\) cuando no tenemos evaluación no es lo mejor, pero como centramos por usuario tiene más sentido hacerlo. Si utilizaramos las calificaciones no centradas, entonces estaríamos suponiendo que las no evaluadas están calificadas muy mal (\(0\), por abajo de \(1\),\(2\),\(3\),\(4\),\(5\)).
Si calculamos similitud entre usuarios de esta forma, las distancia coseno es simplemente el coeficiente de correlación. Nótese que estamos calculando similitud entre items, centrando por usuario, y esto no es lo mismo que correlación entre columnas.
Ejemplo: ¿cómo se ven las calificaciones de películas similares/no similares?
Centramos las calificaciones por usuario y seleccionamos tres películas que pueden ser interesantes.
dat_entrena_c <- dat_entrena %>%
group_by(usuario_id) %>%
mutate(calif_c = calif - mean(calif))
## calculamos un id secuencial.
dat_entrena_c$id_seq <- as.numeric(factor(dat_entrena_c$usuario_id))
filter(pelis_nombres, str_detect(nombre,'Gremlins'))## # A tibble: 3 x 3
## peli_id año nombre
## <dbl> <dbl> <chr>
## 1 2897 1990 Gremlins 2: The New Batch
## 2 6482 1984 Gremlins
## 3 10113 2004 The Wiggles: Whoo Hoo! Wiggly Gremlins!## # A tibble: 2 x 3
## peli_id año nombre
## <dbl> <dbl> <chr>
## 1 2660 1989 When Harry Met Sally
## 2 11850 2003 Dumb and Dumberer: When Harry Met Lloyddat_1 <- filter(dat_entrena_c, peli_id==2897) # Gremlins 2
dat_2 <- filter(dat_entrena_c, peli_id==6482) # Gremlins 1
dat_3 <- filter(dat_entrena_c, peli_id==2660) # WHMSJuntamos usuarios que calificaron cada par:
## Joining, by = "usuario_id"## Joining, by = "usuario_id"Y ahora graficamos. ¿Por qué se ven bandas en estas gráficas?
ggplot(comunes, aes(x=calif_c, y=calif_c_2)) +
geom_jitter(width = 0.2, height = 0.2, alpha = 0.5) +
geom_smooth() + xlab('Gremlins 2') + ylab('Gremlins 1')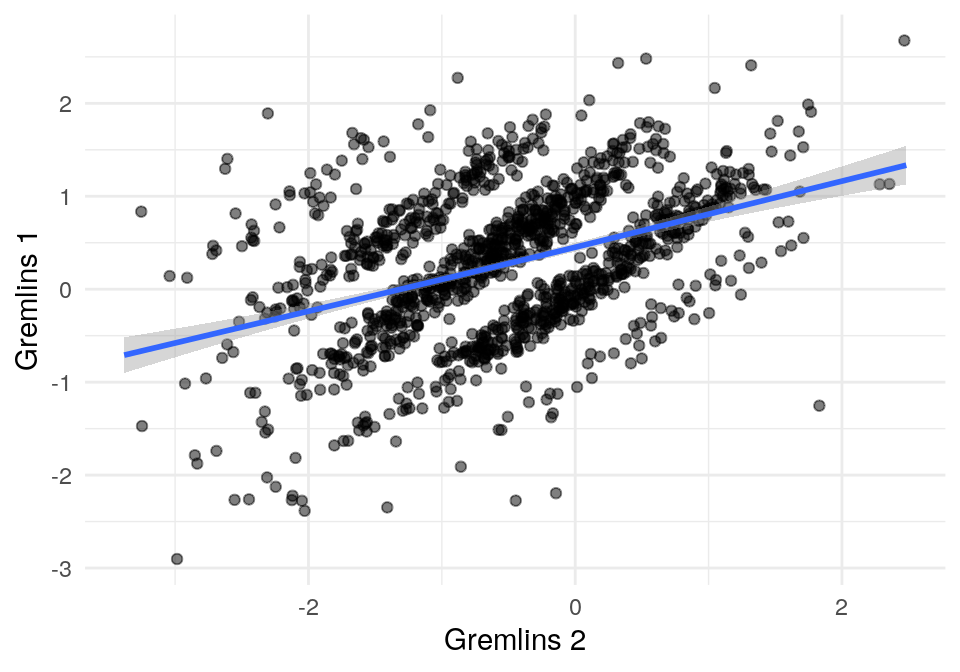
ggplot(comunes_2, aes(x=calif_c, y=calif_c_2)) +
geom_jitter(width = 0.2, height = 0.2, alpha = 0.5) +
geom_smooth() + xlab('Gremlins 2') + ylab('When Harry met Sally')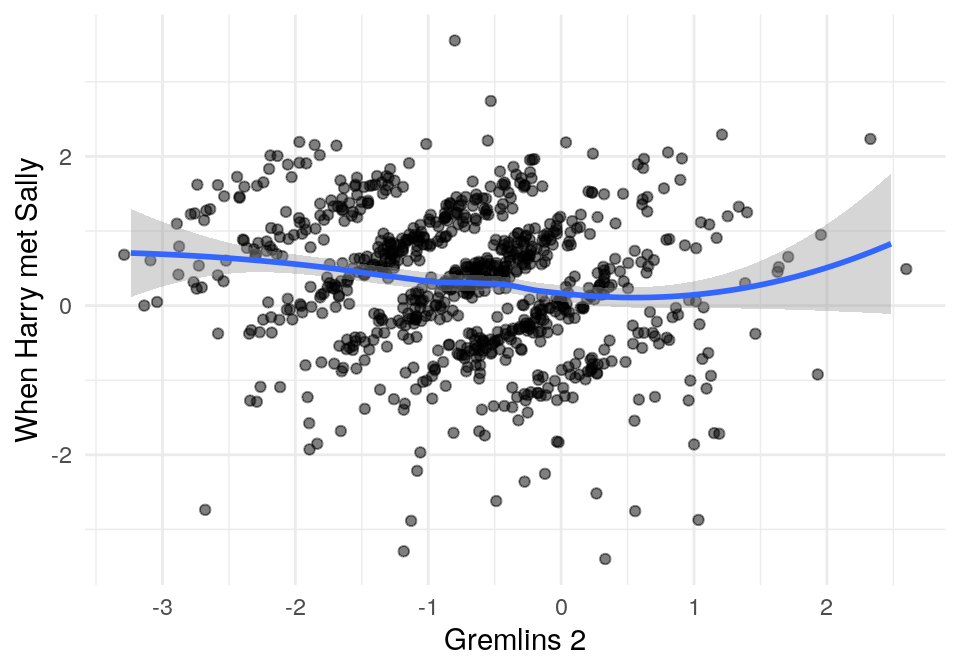
Pregunta: ¿por qué los datos se ven en bandas?
Y calculamos la similitud coseno:
## [1] 0.1769532## [1] -0.3156217Así que las dos Gremlins son algo similares, pero Gremlins \(1\) y Harry Met Sally no son similares.
Podemos ahora seleccionar algunas películas y ver cuáles son películas similares que nos podrían ayudar a hacer recomendaciones:
dat_entrena_2 <- dat_entrena_c %>%
ungroup() %>%
select(peli_id, id_seq, calif_c)
ejemplos <- function(pelicula){
mi_peli <- filter(dat_entrena_2, peli_id==pelicula) %>%
rename(peli_id_1 = peli_id, calif_c_1 = calif_c)
# vamos a calcular todas las similitudes con mi_peli - esto no es buena
# idea y discutiremos más adelante cómo evitarlo
datos_comp <- left_join(dat_entrena_2, mi_peli)
# calcular similitudes
out_sum <- datos_comp %>%
group_by(peli_id) %>%
summarise(dist = sim_cos(calif_c, calif_c_1)) %>%
left_join(medias_p_2)
out_sum %>% arrange(desc(dist)) %>% select(nombre, dist, num_calif_peli)
}Nótese que las similitudes aparentan ser ruidosas si no filtramos por número de evaluaciones:
## Joining, by = "id_seq"Joining, by = "peli_id"| nombre | dist | num_calif_peli |
|---|---|---|
| Larryboy and the Rumor Weed | 1.0000000 | 2 |
| The Purple Rose of Cairo | 1.0000000 | 1379 |
| Invasion: Earth | 1.0000000 | 3 |
| Blood and Black Lace | 0.8231621 | 4 |
| Yes: 35th Anniversary Concert: Songs from Tsongas | 0.7135132 | 14 |
| The Sorrow and the Pity | 0.7011890 | 12 |
| Beauty and the Beast: Special Edition: Bonus Material | 0.6685827 | 15 |
| Street Trash | 0.6541498 | 14 |
| Carpenters: Gold: Greatest Hits | 0.6432310 | 17 |
| The Collected Shorts of Jan Svankmajer: Vol. 2 | 0.6133068 | 10 |
| Sid Caesar Collection: The Fan Favorites | 0.5539756 | 24 |
| The Jack Paar Collection | 0.5323786 | 33 |
| An Occurrence at Owl Creek Bridge | 0.5161915 | 14 |
| Ball of Fire | 0.5095964 | 21 |
| Beckett on Film | 0.4944712 | 16 |
| Christiane F.: A True Story | 0.4854674 | 21 |
| Ivan Vasilievich: Back to the Future | 0.4777115 | 10 |
| Elvis Presley: Great Performances: Vol. 2: The Man and the Music | 0.4725504 | 22 |
| Yaadon Ki Baaraat | 0.4564855 | 27 |
| The Tale of Tsar Saltan | 0.4558849 | 20 |
## Joining, by = "id_seq"Joining, by = "peli_id"| nombre | dist | num_calif_peli |
|---|---|---|
| The Purple Rose of Cairo | 1.0000000 | 1379 |
| Broadway Danny Rose | 0.3531628 | 943 |
| Radio Days | 0.3002320 | 1535 |
| 35 Up | 0.2520458 | 303 |
| Play it Again Sam | 0.2504770 | 1146 |
| Stardust Memories | 0.2490471 | 613 |
| Zelig | 0.2396601 | 1220 |
| Citizen Kane: Bonus Material | 0.2377268 | 201 |
| To Be or Not To Be | 0.2336988 | 212 |
| The Front | 0.2297922 | 319 |
| Wire in the Blood: Season 2 | 0.2257809 | 201 |
| Children of Paradise | 0.2133690 | 356 |
| Umberto D. | 0.2110246 | 290 |
| The Pawnbroker | 0.2002755 | 394 |
| The ’60s | 0.1991641 | 237 |
| Take the Money and Run | 0.1963350 | 1000 |
| Inspector Morse 21: Dead on Time | 0.1920694 | 229 |
| Pather Panchali | 0.1906565 | 291 |
| Yes Minister: Complete Collection | 0.1902482 | 260 |
| Black Narcissus | 0.1872228 | 246 |
## Joining, by = "id_seq"Joining, by = "peli_id"| nombre | dist | num_calif_peli |
|---|---|---|
| 8 1/2 | 1.0000000 | 2075 |
| Larryboy and the Rumor Weed | 1.0000000 | 2 |
| Blood and Black Lace | 0.8204803 | 4 |
| The Land Before Time VI: The Secret of Saurus Rock | 0.7312667 | 2 |
| The Flowers of St. Francis | 0.7299871 | 13 |
| The Sorrow and the Pity | 0.7060662 | 12 |
| Jean Cocteau’s Orphic Trilogy | 0.6551109 | 62 |
| 8.5: Bonus Material | 0.6444320 | 67 |
| An Occurrence at Owl Creek Bridge | 0.6289196 | 14 |
| Curious | 0.6214168 | 11 |
| The Collected Shorts of Jan Svankmajer: Vol. 2 | 0.6213584 | 10 |
| Heimat | 0.5998343 | 6 |
| The BRD Trilogy: Veronika Voss | 0.5909977 | 44 |
| Jacob the Liar | 0.5842952 | 22 |
| Harakiri | 0.5560492 | 34 |
| Trailer Park Boys: Season 4 | 0.5488697 | 6 |
| City War | 0.5446530 | 19 |
| Fat Albert and the Cosby Kids: The Original Animated Series: Vol. 2 | 0.5437757 | 11 |
| Shanghai Shanghai | 0.5301001 | 17 |
| Earth / The End of St. Petersburg / Chess Fever: Triple Feature | 0.5234222 | 23 |
## Joining, by = "id_seq"Joining, by = "peli_id"| nombre | dist | num_calif_peli |
|---|---|---|
| 8 1/2 | 1.0000000 | 2075 |
| La Dolce Vita | 0.4837568 | 1566 |
| Persona | 0.4615395 | 554 |
| Children of Paradise | 0.4491274 | 356 |
| L’Avventura | 0.4208305 | 426 |
| Wild Strawberries | 0.3946798 | 1331 |
| The Rules of the Game | 0.3928481 | 528 |
| Amarcord | 0.3861497 | 810 |
| La Strada: Special Edition | 0.3833987 | 964 |
| Through a Glass Darkly | 0.3772333 | 334 |
| Steamboat Bill Jr. | 0.3745878 | 331 |
| Grand Illusion | 0.3708550 | 821 |
| Band of Outsiders | 0.3615670 | 416 |
| Tokyo Story | 0.3600525 | 389 |
| Rififi | 0.3574095 | 485 |
| Battleship Potemkin | 0.3567248 | 710 |
| Nights of Cabiria | 0.3560156 | 885 |
| The Passion of Joan of Arc | 0.3452051 | 603 |
| Un Chien Andalou | 0.3436363 | 404 |
| Fanny and Alexander (Theatrical Version) | 0.3306075 | 549 |
El problema otra vez es similitudes ruidosas que provienen de pocas evaluaciones en común.
Ejercicio
Intenta con otras películas que te interesen
## Joining, by = "id_seq"Joining, by = "peli_id"## # A tibble: 20 x 3
## nombre dist num_calif_peli
## <chr> <dbl> <int>
## 1 Friends: Season 1 1. 5583
## 2 The Best of Friends: Season 2 0.772 4447
## 3 Friends: Season 4 0.754 4853
## 4 The Best of Friends: Vol. 4 0.749 2334
## 5 Friends: Season 3 0.737 4844
## 6 The Best of Friends: Season 1 0.733 4438
## 7 The Best of Friends: Vol. 3 0.729 2165
## 8 The Best of Friends: Season 3 0.720 4325
## 9 The Best of Friends: Season 4 0.718 3792
## 10 Friends: Season 6 0.712 3975
## 11 Friends: Season 9 0.712 3249
## 12 Friends: Season 7 0.708 3821
## 13 Friends: Season 5 0.705 4386
## 14 The Best of Friends: Vol. 2 0.699 3024
## 15 Friends: Season 8 0.688 3726
## 16 Friends: The Series Finale 0.669 3809
## 17 The Best of Friends: Vol. 1 0.662 4999
## 18 Friends: Season 2 0.586 6206
## 19 Will & Grace: Season 4 0.455 698
## 20 Law & Order: Special Victims Unit: The Second Year 0.426 373## Joining, by = "id_seq"Joining, by = "peli_id"## # A tibble: 20 x 3
## nombre dist num_calif_peli
## <chr> <dbl> <int>
## 1 Anaconda 1. 1955
## 2 Fair Game 0.424 434
## 3 Barb Wire 0.380 425
## 4 House Party 3 0.370 494
## 5 Bats 0.370 510
## 6 Blankman 0.369 618
## 7 Street Fighter 0.366 891
## 8 Vampire in Brooklyn 0.361 824
## 9 Leprechaun 0.354 698
## 10 Home Alone 3 0.353 610
## 11 The Babysitter 0.351 428
## 12 Double Team 0.351 492
## 13 Psycho III 0.350 360
## 14 Godzilla 2000: Millennium 0.346 370
## 15 Universal Soldier: The Return 0.342 915
## 16 Celtic Pride 0.339 492
## 17 House Party 2 0.339 937
## 18 Firestorm 0.338 376
## 19 Pink Cadillac 0.337 312
## 20 Darkman II: The Return of Durant 0.337 394## Joining, by = "id_seq"Joining, by = "peli_id"## # A tibble: 20 x 3
## nombre dist num_calif_peli
## <chr> <dbl> <int>
## 1 When Harry Met Sally 1. 16940
## 2 The Andy Griffith Show: Season 1 0.370 301
## 3 The West Wing: Season 3 0.329 1359
## 4 Anne of Green Gables 0.320 1703
## 5 Doctor Zhivago 0.313 826
## 6 Sex and the City: Season 6: Part 2 0.312 5885
## 7 It's a Wonderful Life 0.311 4588
## 8 Sense and Sensibility 0.309 2325
## 9 The West Wing: Season 2 0.306 1801
## 10 Desk Set 0.302 1266
## 11 Sex and the City: Season 6: Part 1 0.300 6934
## 12 The West Wing: Season 4 0.300 1058
## 13 Friends: Season 9 0.298 3249
## 14 Adam's Rib 0.297 1468
## 15 Pride and Prejudice 0.296 4158
## 16 Sex and the City: Season 5 0.296 6969
## 17 The Sting 0.294 8052
## 18 My So-Called Life 0.293 502
## 19 The Bishop's Wife 0.293 339
## 20 Woman of the Year 0.291 10645.5.2 Implementación
Si queremos implementar este tipo de filtrado colaborativo (por similitud), el ejemplo de arriba no es práctico pues tenemos que calcular todas las posibles similitudes. Sin embargo, como nos interesa principalmente encontrar los pares de similitud alta, podemos usar LSH:
- Empezamos haciendo LSH de las películas usando el método de hiperplanos aleatorios como función hash (pues este es el método que captura distancias coseno bajas). Nuestro resultado son todos los items o películas agrupadas en cubetas. Podemos procesar las cubetas para eliminar falsos positivos (o items con muy pocas evaluaciones).
- Ahora queremos estimar el rating del usuario \(i\) de una película \(j\) que no ha visto. Extraemos las cubetas donde cae la película \(j\), y extraemos todos los items.
- Entre todos estos items, extraemos los que ha visto el usuario \(i\), y aplicamos el promedio (5.1).
Observaciones
- En principio, este análisis podría hacerse usando similitud entre usuarios en lugar de items. En la práctica (ver (Leskovec, Rajaraman, and Ullman 2014)), el enfoque de similitud entre items es superior, pues similitud es un concepto que tiene más sentido en items que en usuarios (los usuarios pueden tener varios intereses traslapados).
- Nótese que en ningún momento tuvimos que extraer variables de películas, imágenes, libros, etc o lo que sea que estamos recomendando. Esta es una fortaleza del filtrado colaborativo.
- Por otro lado, cuando tenemos pocas evaluaciones o calificaciones este método no funciona bien (por ejemplo, no podemos calcular las similitudes pues no hay traslape a lo largo de usuarios). En este caso, este método puede combinarse con otros (por ejemplo, agregar una parte basado en modelos de gusto por género, año, etc.)
5.6 Dimensiones latentes para recomendación
En las similitudes que vimos arriba, es razonable pensar que hay ciertos “conceptos” que agrupan o separan películas, y así mismo, que los usuarios se distinguen por el gusto o no que tienen por estos “conceptos”.
En esta parte, consideramos la idea de utilizar reducción de dimensionalidad para hacer recomendaciones. Esta idea propone que hay ciertos factores latentes (no observados) que describen películas con “contenido implícito similar”, y usuarios según su interés en esa dimensión. Otra manera de llamar estos factores latentes es embedding: buscamos un embedding (una representación numérica en cierta dimensión no muy alta) que nos permita predecir el gusto de un usuario por una película.
Este método nos permitirá también controlar mejor los resultados ruidosos que obtuvimos en los ejemplos anteriores (usando regularización y reducción de dimensión).
5.6.1 Ejemplo: una dimensión latente
Por ejemplo: consideramos una dimensión de películas serias contra películas divertidas. \(3\) películas podrían describirse con
\[v=(-2,0,1)\],
lo que interpretamos como la película \(1\) es divertida (negativa en seriedad-diversión), la película \(2\) está en promedio, y la película \(3\) es más seria que las dos anteriores.
Por otro lado, tenemos descriptores de 5 usuarios:
\[u=(2,3,-3,0,1)\] que dice que a los primeros dos usuarios les gustan las películas serias, al tercero le gustan las divertidas, y los dos últimos no tienen preferencia clara a lo largo de esta dimensión.
Qusiéramos predecir el gusto usando estos dos vectores. Nuestras predicciones (considerando que \(u\) y \(v\) son matrices de una columna) serían simplemente
\[\widetilde{X} = u v^t\]
## [,1] [,2] [,3]
## [1,] -4 0 2
## [2,] -6 0 3
## [3,] 6 0 -3
## [4,] 0 0 0
## [5,] -2 0 1Así que al usuario \(1\) le recomndamos la película \(3\), pero al usuario \(3\) le recomendamos la película \(1\).
La idea es entonces encontrar pesos para películas \(u\) y para usuarios \(v\) de forma que \(X\approx \widetilde{X} = uv^t\): podemos reproducir las calificaciones observadas a partir de nuestro modelo de factores latentes.
Nótese sin embargo que hay varias dimensiones que pueden describir a películas y usuarios: por ejemplo, seria-divertida, artística-hollywood, ciencia ficción, con/sin violencia, etc. Podemos proponer más dimensiones latentes de la siguiente forma:
5.6.2 Ejemplo: dos dimensiones latentes
Tenemos la dimensión anterior de seria-divertida
Y supongamos que tenemos otra dimensión con violencia - sin violencia
Que quiere decir que las películas \(2, 3\) tienen volencia, pero la película \(1\) no. Por otra parte, a los usuarios \(1,2\) y \(5\) no les gustan las películas con violencia, mientras que al usuario \(5\) si les gustan.
La idea ahora es que el gusto de una persona por una película se escribe como combinación de las dos dimensiones. Por ejemplo, para la persona \(1\) tenemos, y la película \(1\), empezamos haciendo
## [1] -4## [1] 9lo que quiere decir que el hecho de que la película \(1\) no sea seria le resta \(4\) en gusto (pues la película \(1\) está del lado “divertido”), pero le suma \(9\) en gusto, pues es una película sin violencia y esta persona está del lado “sin violencia”.
Sumamos para encontrar el gusto total
## [1] 5Para calcular los gustos sobre todas las personas y películas, haríamos
## u_1 u_2
## [1,] 2 -3
## [2,] 3 -3
## [3,] -3 0
## [4,] 0 -2
## [5,] 1 4## v_1 v_2
## [1,] -2 -3
## [2,] 0 2
## [3,] 1 2## [,1] [,2] [,3]
## [1,] 5 -6 -4
## [2,] 3 -6 -3
## [3,] 6 0 -3
## [4,] 6 -4 -4
## [5,] -14 8 9- El renglón \(j\) de \(U\) son los valores en las dimensiones latentes para la película \(i\) (descriptores de usuarios).
- El renglón \(j\) de \(V\) son los valores en las dimensiones latentes para el usuario \(j\) (descriptores de películas)
Con \(k\) dimensiones latentes, el modelo que proponemos es:
\[\widetilde{X} = UV^t\]
donde \(U\) es una matrix de \(n\times k\) (\(n=\) número de usuarios), y \(V\) es una matriz de \(p \times k\), donde \(p\) es el número de películas.
Buscamos que, si \(X\) son las verdaderas calificaciones, entonces \[X\approx \widetilde{X}.\]
y nótese que esta aproximación es en el sentido de las entradas de \(X\) que son observadas. Sin embargo, \(\widetilde{X}\) nos da predicciones para todos los pares película-persona.Bajo este modelo, la predicción para el usuario \(i\) y la película \(j\) es la siguiente suma sobre las dimensiones latentes:
\[\widetilde{x}_{ij} =\sum_k u_{ik} v_{jk}\]
que expresa el hecho de que el gusto de \(i\) por \(j\) depende de una combinación (suma) de factores latentes de películas ponderados por gusto por esos factores del usuario.
El número de factores latentes \(k\) debe ser seleccionado (por ejemplo, según el error de validación). Dado \(k\), para encontrar \(U\) y \(V\) (un total de \(k(n+p)\) parámetros) buscamos minimizar
\[\sum_{(i,j)\, obs} (x_{ij}-\widetilde{x}_{ij})^2,\]
que también podemos escribir este problema (recuérdese que \(u_i\) y \(v_j\) aquí son vectores renglón) como
\[\min_{U,V}\sum_{(i,j)\, obs} (x_{ij}-u_iv_j^t)^2\] donde \(u_i\) es el renglón \(i\)-esimo de \(U\) (gustos latentes del usuario \(i\) en cada dimensión), y \(v_j\) es el renglón \(j\)-ésimo de la matriz \(V\) (calificación latente de la película en cada dimensión)
¿Por qué funciona la idea de factores latentes?
El método de factorización de matrices de grado bajo (\(k\)) funciona compartiendo información a lo largo de películas y usuarios. Como tenemos que ajustar los datos observados, y solo tenemos a nuestra disposición \(k\) descriptores para cada película y usuario, una minimización exitosa captura regularidades en los datos.
- Es importante que la representación sea de grado relativamente bajo, pues esta “compresión” es la que permite que las dimensiones latentes capturen regularidades que están en los datos observados (que esperamos encontrar en el proceso de ajuste).
Por ejemplo, supongamos que el gusto por las películas sólo depende de una dimensión sería - divertida. Si ajustamos un modelo de un solo factor latente, un mínimo se alcanzaría separando con la dimensión latente las películas serias de las divertidas, y los usuarios que prefieren películas serias o divertidas. Esta sería una buena explicación de los datos observados, y las predicciones para películas no vistas sería buena usando simplemente el valor en seriedad de la película (extraída de otras personas con gustos divertido o serio) y el gusto por seriedad de esa persona (extraida de la observación de que le gustan otras películas serias u otras divertidas).
5.6.3 Combinación con modelo base
Podemos usar también ideas de nuestro modelo base y modelar desviaciones en lugar de calificaciones directamente:
Si \(X^0\) son las predicciones del modelo de referencia, y \[R = X-X^0\] son los residuales del modelo base, buscamos mejor \[R\approx \widetilde{X} = UV^t\] de manera que las predicciones finales son \[X^0 + \widetilde{X}\]
Veremos también más adelante cómo regularizar estos sesgos como parte de la construcción del modelo.
5.7 Factorización de matrices
Como vimos arriba, reexpresamos nuestro problema como un problema de factorización de matrices (encontrar \(U\) y \(V\)). Hay varias alternativas populares para atacarlo:
- Descomposición en valores singulares (SVD).
- Mínimos cuadrados alternados.
- Descenso en gradiente estocástico.
Para entender más del primer enfoque, puedes consultar por ejemplo las notas del curso de aprendizaje de máquina https://github.com/felipegonzalez/aprendizaje-maquina-mcd/blob/master/14-reducir-dimensionalidad.Rmd. No vamos a ver más de este enfoque, pues no es del todo apropiado: nuestras matrices tienen muchos datos faltantes, y SVD naturalmente no está diseñado para lidiar con este problema. Se pueden hacer ciertas imputaciones (por ejemplo, insertar 0’s una vez que centramos por usuario), pero los siguientes dos métodos están mejor adaptados para nuestro problema.
5.8 Mínimos cuadrados alternados
Supongamos entonces que queremos encontrar matrices \(U\) y \(V\), donde \(U\) es una matrix de \(n \times k\) (\(n=\) número de usuarios), y \(V\) es una matriz de \(p \times k\), donde \(p\) es el número de películas que nos de una aproximación de la matrix \(X\) de calificaciones \[ X \approx UV^t \] Ahora supongamos que conocemos \(V_1\). Si este es el caso, entonces queremos resolver para \(U_1\): \[ \min_{U_1}|| X - U_1V_1^t||_{obs}^2\] Como \(V_1^t\) están fijas, este es un problema de mínimos cuadrados usual, y puede resolverse analíticamente (o usar descenso en gradiente, que es simple de calcular de forma analítica) para encontrar \(U_1\). Una vez que encontramos \(U_1\), la fijamos, e intentamos ahora resolver para \(V\):
\[ \min_{V_2}|| X - U_1V_2^t||_{obs}^2\] Y una vez que encontramos \(V_2\) resolvemos
\[ \min_{U_2}|| X - U_2V_2^t||_{obs}^2\]
Continuamos este proceso hasta encontrar un mínimo local o hasta cierto número de iteraciones. Para inicializar \(V_1\), en (Zhou et al. 2008) se recomienda tomar como primer renglón el promedio de las calificaciones de las películas, y el resto números aleatorios chicos (por ejemplo \(U(0,1)\)). También pueden inicializarse con números aleatorios chicos las dos matrices.
5.8.1 Mínimos cuadrados alternados con regularización
Para agregar regularización y lidiar con los datos ralos, podemos incluir un coeficiente adicional. Minimizamos entonces (como en (Zhou et al. 2008)):
\[\min_{U,V}\sum_{(i,j)\, obs} (x_{ij}-u_i^tv_j)^2 + \lambda \left ( \sum_i n_{i}||u_i||^2 + \sum_j m_{j} ||v_j||^2 \right)\]
y modificamos de manera correspondiente cada paso de mínimos cuadrados mostrado arriba. \(n_{i}\) es el número de evaluaciones del usuario \(i\), y \(m_j\) es el número de evaluaciones de la película \(j\).
Observaciones:
- Nótese que penalizamos el tamaños de los vectores \(u_i\) y \(v_j\) para evitar sobreajuste (como en regresión ridge).
- Nótese también que los pesos \(n_i\) y \(m_j\) en esta regularización hace comparables el término que aparece en la suma de los residuales al cuadrado (la primera suma), y el término de regularización: por ejemplo, si el usuario \(i\) hizo \(n_i\) evaluaciones, entonces habrá \(n_i\) términos en la suma de la izquierda. Lo mismo podemos decir acerca de las películas.
- Este no es el único término de regularización posible. Por ejemplo, podríamos no usar los pesos \(n_i\) y \(m_j\), y obtendríamos un esquema razonable también, donde hay más regularización relativa para usuarios/películas que tengan pocas evaluaciones.
Este método está implementado en spark. La implementación está basada parcialmente en (Zhou et al. 2008). La inicialización es diferente en spark, ver el código, donde cada renglón se inicializa con un vector de \(N(0,1)\) normalizado.
En este caso, copiamos nuestra tabla a spark (nota: esto es algo que normalmente no haríamos, los datos habrían sido cargados en el cluster de spark de otra forma):
rm(list = c('dat_netflix', 'dat_entrena_2','dat_entrena_c'))
library(tidyverse)
library(sparklyr)
# configuración para spark
config <- spark_config()
config$`spark.env.SPARK_LOCAL_IP.local` <- "0.0.0.0"
config$`sparklyr.shell.driver-memory` <- "6G"
config$spark.executor.memory <- "1G"# conectar con "cluster" local
sc <- spark_connect(master = "local", config = config)
spark_set_checkpoint_dir(sc, './checkpoint')dat_tbl <- spark_read_csv(sc, name="netflix", "../datos/netflix/dat_muestra_nflix.csv")
dat_tbl <- dat_tbl %>% select(-fecha)usuario_val <- dat_tbl %>% select(usuario_id) %>%
distinct() %>%
sdf_sample(fraction = 0.1) %>% compute("usuario_val")
pelicula_val <- dat_tbl %>% select(peli_id) %>%
distinct() %>%
sdf_sample(fraction = 0.1) %>% compute("pelicula_val")
valida_tbl <- dat_tbl %>%
inner_join(usuario_val) %>%
inner_join(pelicula_val) %>%
compute("valida_tbl")## Joining, by = "usuario_id"Joining, by = "peli_id"## Joining, by = c("peli_id", "usuario_id_orig", "calif", "usuario_id")## # Source: spark<?> [?? x 1]
## n
## <dbl>
## 1 20788821## # Source: spark<?> [?? x 1]
## n
## <dbl>
## 1 195774Vamos a hacer primero una descomposición en \(15\) factores, con regularización relativamente alta:
modelo <- ml_als(entrena_tbl,
rating_col = 'calif',
user_col = 'usuario_id',
item_col = 'peli_id',
rank = 15, reg_param = 0.1,
checkpoint_interval = 5,
max_iter = 50)
# Nota: checkpoint evita que la gráfica de cálculo
# sea demasiado grande. Cada 5 iteraciones hace una
# nueva gráfica con los resultados de la última iteración.## ALSModel (Transformer)
## <als_6a75d8d3db1>
## (Parameters -- Column Names)
## cold_start_strategy: nan
## item_col: peli_id
## prediction_col: prediction
## user_col: usuario_id
## (Transformer Info)
## item_factors: <tbl_spark>
## rank: int 15
## recommend_for_all_items: <function>
## recommend_for_all_users: <function>
## user_factors: <tbl_spark>Hacemos predicciones para el conjunto de validación:
preds <- ml_predict(modelo, valida_tbl) %>%
mutate(prediction = ifelse(isnan(prediction), 3.5, prediction))
ml_regression_evaluator(preds, label_col = "calif", prediction_col = "prediction",
metric_name = "rmse")## [1] 0.8742091Y podemos traer a R los datos de validación (que son chicos) para examinar:
preds_df <- preds %>% collect() #traemos a R con collect
ggplot(preds, aes(x = prediction)) + geom_histogram()## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.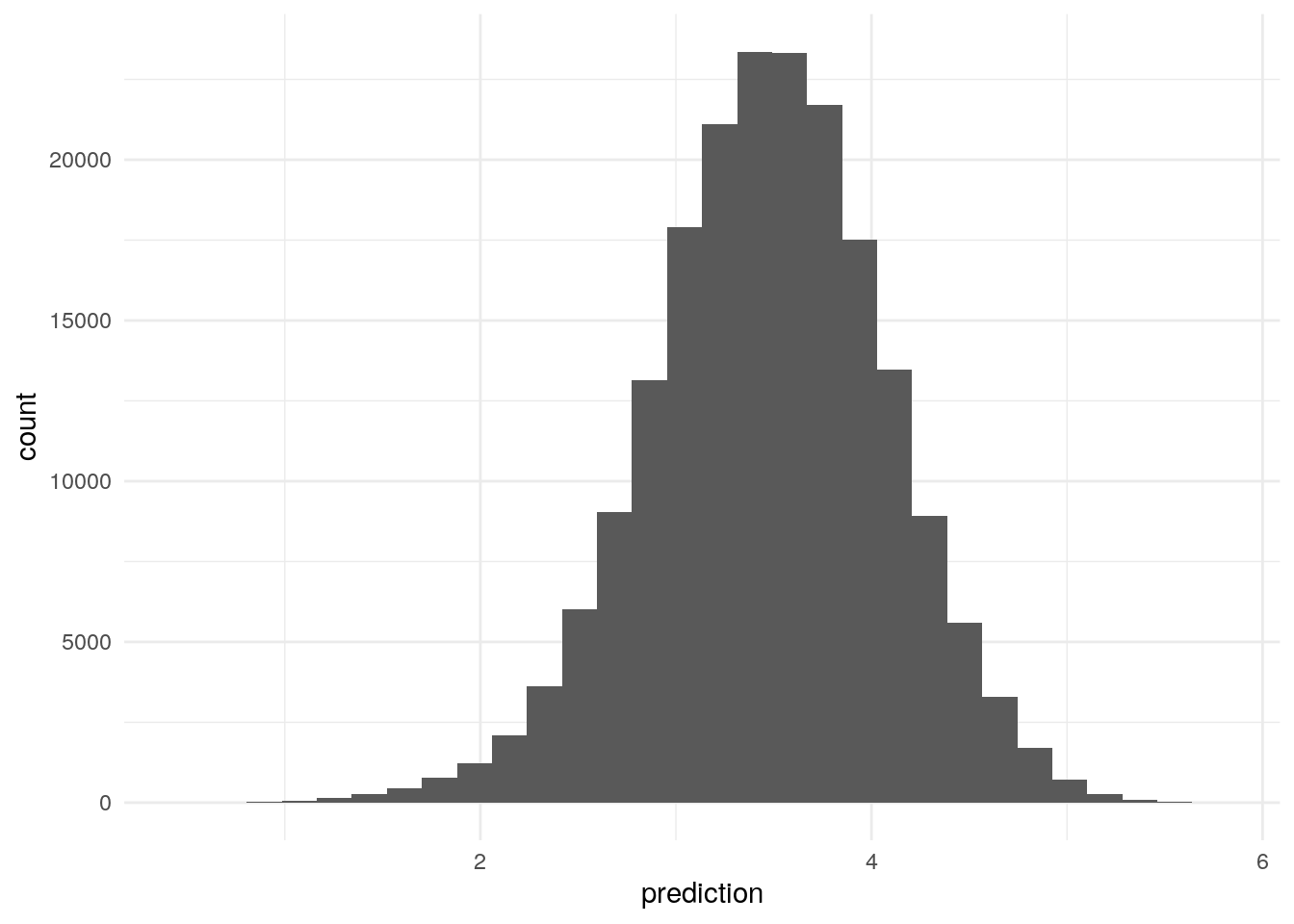
Y redujimos considerablemente el error del modelo base. Examinamos ahora las dimensiones asociadas con películas:
## # Source: spark<?> [?? x 17]
## id features features_1 features_2 features_3 features_4 features_5
## <int> <list> <dbl> <dbl> <dbl> <dbl> <dbl>
## 1 10 <list [… 0.292 0.418 -0.637 0.100 -0.746
## 2 20 <list [… 0.441 -0.251 -1.04 -0.00424 -0.0171
## 3 30 <list [… 0.162 0.0277 -0.723 0.0924 -0.381
## 4 40 <list [… 0.203 -0.135 -0.824 0.142 -0.0909
## 5 50 <list [… -0.0218 0.0762 -0.912 -0.00859 -0.231
## 6 60 <list [… 0.286 0.367 -0.532 -0.0261 -0.738
## 7 70 <list [… 0.314 0.0129 -0.696 0.141 -0.838
## 8 80 <list [… 0.227 -0.0451 -0.977 0.759 -0.564
## 9 90 <list [… 0.163 -0.148 -0.913 -0.0698 -0.219
## 10 100 <list [… 0.213 -0.110 -0.674 -0.00461 -0.200
## # … with more rows, and 10 more variables: features_6 <dbl>, features_7 <dbl>,
## # features_8 <dbl>, features_9 <dbl>, features_10 <dbl>, features_11 <dbl>,
## # features_12 <dbl>, features_13 <dbl>, features_14 <dbl>, features_15 <dbl>Nota: La columna features contiene la misma información de feature_1,feature_2,…, pero en forma de lista.
Examinemos la interpretación de los factores latentes de las películas.
medias_peliculas <- entrena_tbl %>% group_by(peli_id) %>%
summarise(num_calif_peli = n(), media_peli = mean(calif)) %>%
collect()## Warning: Missing values are always removed in SQL.
## Use `mean(x, na.rm = TRUE)` to silence this warning
## This warning is displayed only once per session.latentes_pelis <- V_df %>%
rename(peli_id = id) %>%
left_join(pelis_nombres %>% left_join(medias_peliculas))## Joining, by = "peli_id"Joining, by = "peli_id"Para la primera dimensión latente:
top_tail <- function(latentes_pelis, feature){
top_df <- arrange(latentes_pelis, {{ feature }} ) %>%
select(nombre, {{ feature }}, media_peli, num_calif_peli) %>%
filter(num_calif_peli > 2000) %>%
head(100)
tail_df <- arrange(latentes_pelis, {{ feature }} ) %>%
select(nombre, {{ feature }}, media_peli, num_calif_peli) %>%
filter(num_calif_peli > 2000) %>%
tail(100)
print(top_df)
print(tail_df)
bind_rows(top_df, tail_df)
}
res <- top_tail(latentes_pelis, features_1)## # A tibble: 100 x 4
## nombre features_1 media_peli num_calif_peli
## <chr> <dbl> <dbl> <dbl>
## 1 The Princess Diaries (Widescreen) -0.295 3.57 15020
## 2 Miss Congeniality -0.273 3.37 44038
## 3 Bride and Prejudice -0.254 3.27 2354
## 4 The Wedding Planner -0.251 3.19 29347
## 5 The Princess Diaries (Fullscreen) -0.243 4.06 4434
## 6 Maid in Manhattan -0.222 3.16 26442
## 7 New York Minute -0.213 3.04 2680
## 8 Sweet Home Alabama -0.207 3.54 36787
## 9 The Princess Diaries 2: Royal Engagement -0.198 3.72 9384
## 10 Emma -0.197 3.66 4619
## # … with 90 more rows
## # A tibble: 100 x 4
## nombre features_1 media_peli num_calif_peli
## <chr> <dbl> <dbl> <dbl>
## 1 Rocky 0.601 3.77 16150
## 2 American History X 0.601 4.20 14694
## 3 Beavis and Butt-head Do America 0.601 3.28 2920
## 4 For a Few Dollars More 0.601 4.02 3552
## 5 The General's Daughter 0.601 3.36 24487
## 6 Swordfish 0.602 3.35 28795
## 7 Hannibal 0.603 3.46 10793
## 8 Leaving Las Vegas 0.603 3.57 8165
## 9 The Sopranos: Season 4 0.603 4.48 6559
## 10 From Dusk Till Dawn 0.604 3.45 5562
## # … with 90 more rowsLa segunda dimensión latente:
## # A tibble: 100 x 4
## nombre features_2 media_peli num_calif_peli
## <chr> <dbl> <dbl> <dbl>
## 1 The Best of Friends: Vol. 2 -1.05 4.11 3024
## 2 The Best of Friends: Season 1 -1.03 4.15 4438
## 3 The Best of Friends: Season 2 -1.02 4.14 4447
## 4 Friends: Season 4 -1.02 4.15 4853
## 5 Friends: The Series Finale -1.02 4.12 3809
## 6 The Best of Friends: Season 3 -1.01 4.17 4325
## 7 Friends: Season 1 -1.01 4.10 5057
## 8 Friends: Season 3 -0.996 4.08 4844
## 9 The Best of Friends: Season 4 -0.985 4.26 3792
## 10 Friends: Season 5 -0.984 4.23 4386
## # … with 90 more rows
## # A tibble: 100 x 4
## nombre features_2 media_peli num_calif_peli
## <chr> <dbl> <dbl> <dbl>
## 1 The Manchurian Candidate 0.246 3.86 7736
## 2 Vertigo 0.246 4.05 9285
## 3 Coffee and Cigarettes 0.246 2.65 2714
## 4 The Barbarian Invasions 0.246 3.61 2332
## 5 13 Conversations About One Thing 0.247 3.23 2303
## 6 Metropolis 0.248 3.88 2174
## 7 Swimming Pool 0.248 3.14 5962
## 8 My Left Foot: Special Edition 0.250 3.95 2165
## 9 The Graduate 0.250 3.93 16536
## 10 From Here to Eternity 0.250 3.75 2798
## # … with 90 more rowsNota: Podemos usar ml_recommend para producir recomendaciones de películas para usuarios, o para cada película los usuarios más afines.
## [1] 1Ejercicio
Examina otras dimensiones latentes, ¿qué puedes interpretar?
5.9 Descenso en gradiente estocástico
En esta parte veremos otra manera de construir factorización de matrices para filtrado colaborativo, usando descenso en gradiente estocástico. Este método es similar a mínimos cuadrados alternados (ALS).
Para un recordatorio de descenso en gradiente, y la versión estocástica, puedes ver por ejemplo, el artículo de wikipedia - Stochastic Gradient Descent o las notas de aprendizaje de máquina.
Consideremos el problema de factorización que queremos resolver. Si \(X\) (\(n\times p\)) es la matriz de calificaciones, quisieramos encontrar matrices \(U\) y \(V\) (de tamaños \(n\times k\) y \(p\times k\)) tales que \[X\approx UV^t,\] donde los reglones de \(U\) son los descriptores de los usuarios y los renglones de \(V\) son los descriptores de las películas (ver sección anterior). Más expecíficamente, buscamos minimizar
\[\begin{equation} \min_{U,V} \sum_{(i,j) obs} (x_{ij} - u_iv_j^t)^2 \end{equation}\] donde \(u_i\) es el renglón \(i\)-ésimo de \(U\) y \(v_j\) es el renglón \(j\)-ésimo de \(V\). En términos de sus componentes, queremos minimizar
\[\begin{equation} L = \sum_{(i,j) obs} (x_{ij} - \sum_{l=1}^k u_{i,l}v_{j,l})^2 \end{equation}\]
Escribimos \[ L_{i,j} = e_{i,j}^2 = (x_{ij} - \sum_{l=1}^k u_{i,l}v_{j,l})^2\].
Para encontrar el gradiente, derivamos con respecto a cada parámetro (\(u_{i,l}\) y \(v_{j,l}\)). Empezamos con cada término \(L_{i,j}\):
\[\frac{\partial L_{i,j}}{\partial u_{i,s}} = -2e_{i,j} v_{j,s} \]
y \[\frac{\partial L_{i,j}}{\partial v_{j,t}} = -2e_{i,j} u_{i,t} \]
El resto de las derivadas son iguales a \(0\) (para otros \(u_a^{(m)}\), \(v_b^{(m)}\)). Esto nos da la dirección del gradiente en cada paso del descenso estocástico.
Sea \(\gamma >0\) el tamaño de paso (tasa de aprendizaje) de descenso estocástico. Para cada evaluación \(x_{i,j}\), la actualización de descenso está dada por, en forma vectorial:
\[ u_i^{(n+1)} = u_i^{(n)} +\gamma e_{i,j} v_j^{(n)} \] y \[ v_j^{(n+1)} = v_j^{(n)} +\gamma e_{i,j} u_j^{(n)} \]
Inicializamos las matrices \(U\) y \(V\) con valores aleatorios chicos.5.9.1 Agregando el modelo base (sesgos)
Podemos también agregar el modelo base (que a veces es llamado modelo con sesgos):
\[\begin{equation} L = \sum_{(i,j) obs} (x_{ij} - a_i - b_j - \sum_{l=1}^k u_{i}^{(l)}v_{j}^{(l)})^2 \end{equation}\]
Y las derivadas adicionales están dadas por
\[\frac{\partial L_{i,j}}{\partial a_i} = -2e_{i,j} \]
\[\frac{\partial L_{i,j}}{\partial b_j} = -2e_{i,j} \]
y el resto de las derivadas (para otras \(a_s\) y \(b_t\)) son iguales a \(0\).
- Nótese que en cada paso de descenso estocástico, las actualizaciones sólo involucran los parámetros asociados con el usuario/película que estamos evaluando, y el cálculo es simple.
- No necesitamos tener en memoria todos los datos, podemos leerlos en lotes y procesar cada lote sucesivemante.
5.9.2 Regularización
Finalmente, podemos agregar regularización para controlar el sobreajuste (por ejemplo, usuarios con pocas evaluaciones, o películas con pocas evaluaciones).
La función a minimizar es ahora
\[\begin{equation} L = \sum_{(i,j) obs} (x_{ij} - \mu - a_i - b_j - \sum_{l=1}^k u_{i,l}v_{j,l})^2 + \lambda \left ( \sum_i ||u_i||^2 + \sum_j ||v_j||^2 + \sum_i a_i^2 + \sum_j b_j^2 \right ) \tag{5.2} \end{equation}\]
donde también es posible usar parámetros de regularización distintos (\(\lambda\)) para los vectores y los sesgos.
Sea \(\gamma >0\) el tamaño de paso (tasa de aprendizaje) de descenso estocástico, y \(\lambda \geq 0\) una constante de regularización. Sea \(n_i\) el número de evaluaciones del usuario \(i\) y \(m_j\) el número de evaluaciones para la película \(j\). Para cada evaluación \(x_{i,j}\), la actualización de descenso está dada, en forma vectorial, por:
\[ u_i^{(n+1)} = u_i^{(n)} + \gamma \left ( e_{i,j} v_j^{(n)} - \frac{\lambda}{n_i} u_i^{(n)} \right ) \]
y
\[ v_j^{(n+1)} = v_j^{(n)} + \gamma \left ( e_{i,j} u_j^{(n)} - \frac{\lambda}{m_j} v_j^{(n)} \right ) \]
Para los sesgos, las actualizaciones son (no regularizamos la media global):
\[\mu^{(n+1)} = \mu^{(n)} + \gamma e_{i,j}\]
\[a_i^{(n+1)} = a_i^{(n)} + \gamma \left ( e_{i,j} - \frac{\lambda}{n_i} a_i^{(n)} \right )\]
\[b_j^{(n+1)} = b_i^{(n+1)} + \gamma \left ( e_{i,j} - \frac{\lambda}{m_j} b_j^{(n)} \right )\]
Inicializamos las matrices \(U\) y \(V\) con valores aleatorios chicos.Puedes ver este video, de los autores de nuestro libro de texto
Nótese que dividimos entre el número de evaluaciones de usuarios y películas a la constante de regularización. Esto se puede entender observando que el término de regularización en (5.2) se puede poner bajo la suma dividiendo por estos factores. También se puede observar que el valor esperado del gradiente calculado de esta manera es (5.2) (excepto por un factor constante).
Este es un tipo de regularización distinto al que usamos en el ejemplo de mínimos cuadrados alternados.
5.9.3 Ejemplo (Netflix)
Usaremos una implementación en C++ para tener mejor desempeño (una introducción a extensiones de C++ para R está en (Wickham 2014)).
library(Rcpp)
Rcpp::sourceCpp('../src/factorizacion_mat/descenso_estocastico.cpp')
Rcpp::sourceCpp('../src/factorizacion_mat/calc_error_bias.cpp')#include <Rcpp.h>
using namespace Rcpp;
// [[Rcpp::export]]
List descenso_estocastico(NumericVector i_idx, NumericVector j_idx, NumericVector x,
NumericMatrix U, NumericMatrix V, double mu,
NumericVector a, NumericVector b,
double gamma, double lambda_mat,
double lambda_sesgos, int n_iter,
NumericVector num_peli, NumericVector num_usu) {
double e;
NumericVector i = i_idx - 1;
NumericVector j = j_idx - 1;
NumericVector U_row;
NumericVector V_row;
for(int iter = 0; iter < n_iter; iter++){
for(int t = 0; t < i.size(); t++){
//Rcout << "Numero de usuario " << i(t) ;
//Rcout << "Numero de pelicula " << j(t) << std::endl;
e = x(t) - mu - a(i(t)) - b(j(t)) - sum(U(i(t), _) * V(j(t), _) );
U_row = U(i(t), _);
V_row = V(j(t), _);
U(i(t), _) = U_row + gamma*(e * V_row - (lambda_mat / num_usu(i(t))) * U_row);
V(j(t), _) = V_row + gamma*(e * U_row - (lambda_mat / num_peli(j(t))) * V_row);
a(i(t)) = a(i(t)) + gamma*(e - (lambda_sesgos / num_usu(i(t))) * a(i(t)));
b(j(t)) = b(j(t)) + gamma*(e - (lambda_sesgos / num_peli(j(t)))* b(j(t)));
mu = mu + gamma * e;
}
}
return List::create(Rcpp::Named("U") = U,
Rcpp::Named("V") = V,
Rcpp::Named("a") = a,
Rcpp::Named("b") = b);
}Por ejemplo:
##
## Attaching package: 'Matrix'## The following objects are masked from 'package:tidyr':
##
## expand, pack, unpack# entrenamiento
set.seed(1182)
#permutamos para las rondas de descenso estocástico
permutacion <- sample(1:length(dat_entrena$usuario_id),
length(dat_entrena$usuario_id))
i <- dat_entrena$usuario_id[permutacion]
j <- dat_entrena$peli_id[permutacion]
y <- dat_entrena$calif[permutacion]
# validación
i_val <- dat_valida$usuario_id
j_val <- dat_valida$peli_id
y_val <- dat_valida$califPodemos agregar también dos usuarios nuevos con evaluaciones opuestas (puedes llenar con tus preferencias)
i_usuario_1 <- rep(100001, 12)
i_usuario_2 <- rep(100002, 12)
nombres_evaluar <- data_frame(nombre =
c('Ghost', 'Pretty Woman', 'Driving Miss Daisy',
'The Fast and the Furious', 'Meet the Fockers',
'Independence Day', 'Top Gun',
'Being John Malkovich', 'A Clockwork Orange',
'Fight Club', 'Pulp Fiction',
'The Terminator'))
evals_1 <- c(1, 2, 2, 4, 3, 4, 4, 2, 4, 5, 5, 5)
evals_2 <- 6 - evals_1
nombres_evaluar$evals <- evals_1
nombres_evaluar## # A tibble: 12 x 2
## nombre evals
## <chr> <dbl>
## 1 Ghost 1
## 2 Pretty Woman 2
## 3 Driving Miss Daisy 2
## 4 The Fast and the Furious 4
## 5 Meet the Fockers 3
## 6 Independence Day 4
## 7 Top Gun 4
## 8 Being John Malkovich 2
## 9 A Clockwork Orange 4
## 10 Fight Club 5
## 11 Pulp Fiction 5
## 12 The Terminator 5## Joining, by = "nombre"i <- c(i, i_usuario_1, i_usuario_2)
j <- c(j, j_evaluar, j_evaluar)
y <- c(y, evals_1, evals_2)
X <- sparseMatrix(i, j, x = y, dims=c(max(i), 17770))
dim(X)## [1] 100002 17770#otra manera de inicializar es con resultados de SVD
#library(irlba)
#test <- irlba(X, nv = 4, nu = 4)
#U_0 <- test$u%*%sqrt(diag(test$d))
#V_0 <- test$v%*%sqrt(diag(test$d))
#inicialización
set.seed(2805)
U_0 <- matrix(rnorm(4 * max(i), 0, 0.01), ncol = 4)
V_0 <- matrix(rnorm(4 * 17770, 0, 0.01), ncol = 4)
U <- U_0
V <- V_0
num_usu <- rowSums(X>0) + 1
num_peli <- colSums(X>0) + 1
mu <- mean(y)
a <- rowSums(X)/rowSums(X>0) - mean(y)
a[is.nan(a)] <- 0
b <- colSums(X)/colSums(X>0) - mean(y)
print(sqrt(calc_error(i, j, y, U, V, mu, a, b)))## [1] 0.9224815for(iter in 1:10){
# nota: la función descenso_gradiente (C++) no hace copias de U,V,a,b
# cambia in-place estos parámetros
salida <- descenso_estocastico(i, j, y, U, V, mu, a, b,
gamma = 0.004, lambda_mat = 20, lambda_sesgos = 20,
n_iter = 1, num_peli, num_usu)
error_entrena <- sqrt(calc_error(i, j, y, U, V, mu, a, b))
error_valida <- sqrt(calc_error(i_val, j_val, y_val, U, V, mu, a, b))
sprintf("Iteración: %i, Error entrena: %.4f, Error valida: %.4f",
iter,
error_entrena, error_valida) %>% print
}## [1] "Iteración: 1, Error entrena: 0.9166, Error valida: 0.9231"
## [1] "Iteración: 2, Error entrena: 0.9158, Error valida: 0.9221"
## [1] "Iteración: 3, Error entrena: 0.9113, Error valida: 0.9193"
## [1] "Iteración: 4, Error entrena: 0.8915, Error valida: 0.9047"
## [1] "Iteración: 5, Error entrena: 0.8848, Error valida: 0.8985"
## [1] "Iteración: 6, Error entrena: 0.8791, Error valida: 0.8942"
## [1] "Iteración: 7, Error entrena: 0.8712, Error valida: 0.8885"
## [1] "Iteración: 8, Error entrena: 0.8650, Error valida: 0.8839"
## [1] "Iteración: 9, Error entrena: 0.8623, Error valida: 0.8818"
## [1] "Iteración: 10, Error entrena: 0.8614, Error valida: 0.8812"usuario_1_u <- U[100001, ]
prefs_1 <- mu + a[100001] + b + V %*% usuario_1_u %>% as.numeric
prefs <- data_frame(prefs = prefs_1, peli_id = 1:17770) %>%
left_join(medias_pelis, by = 'peli_id') %>%
arrange(desc(prefs)) %>%
filter(num_calif_peli > 500) %>%
select(peli_id, nombre, prefs) %>% top_n(100, prefs)
DT::datatable(prefs)usuario_2_u <- U[100002, ]
prefs_2 <- mu + a[100002] + b + V %*% usuario_2_u %>% as.numeric
prefs <- data_frame(prefs = prefs_2, peli_id = 1:17770) %>%
left_join(medias_pelis) %>%
arrange(desc(prefs)) %>%
filter(num_calif_peli > 500) %>%
select(nombre, prefs) %>% top_n(100, prefs) ## Joining, by = "peli_id"Filtramos para ver películas bien conocidas, y muestreamos para empezar a entender el significado de las dimensiones:
## Warning: `as_data_frame()` is deprecated, use `as_tibble()` (but mind the new semantics).
## This warning is displayed once per session.## Joining, by = "peli_id"set.seed(1221)
muestra_graf <- V_df %>%
filter(num_calif_peli > 20000) %>%
sample_n(100)
ggplot(muestra_graf,
aes(x = V1, y= V2, label=nombre, colour=media_peli))+
geom_point() + geom_text_repel(size=3.5, segment.alpha = 0.3, direction = 'y')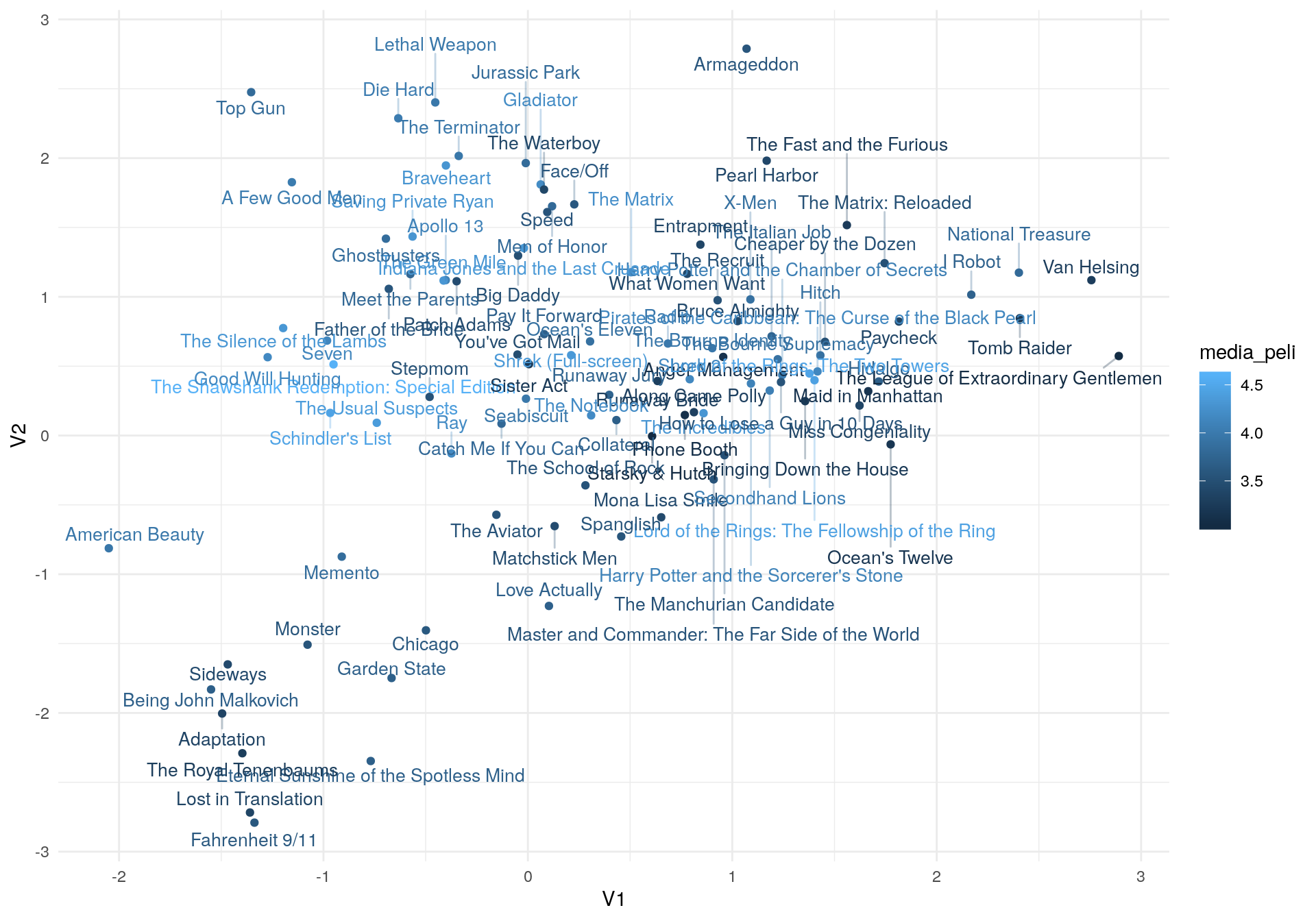
ggplot(muestra_graf,
aes(x = V3, y= V4, label=nombre, colour=media_peli))+
geom_point() + geom_text_repel(size=3.5, segment.alpha = 0.3, direction='y')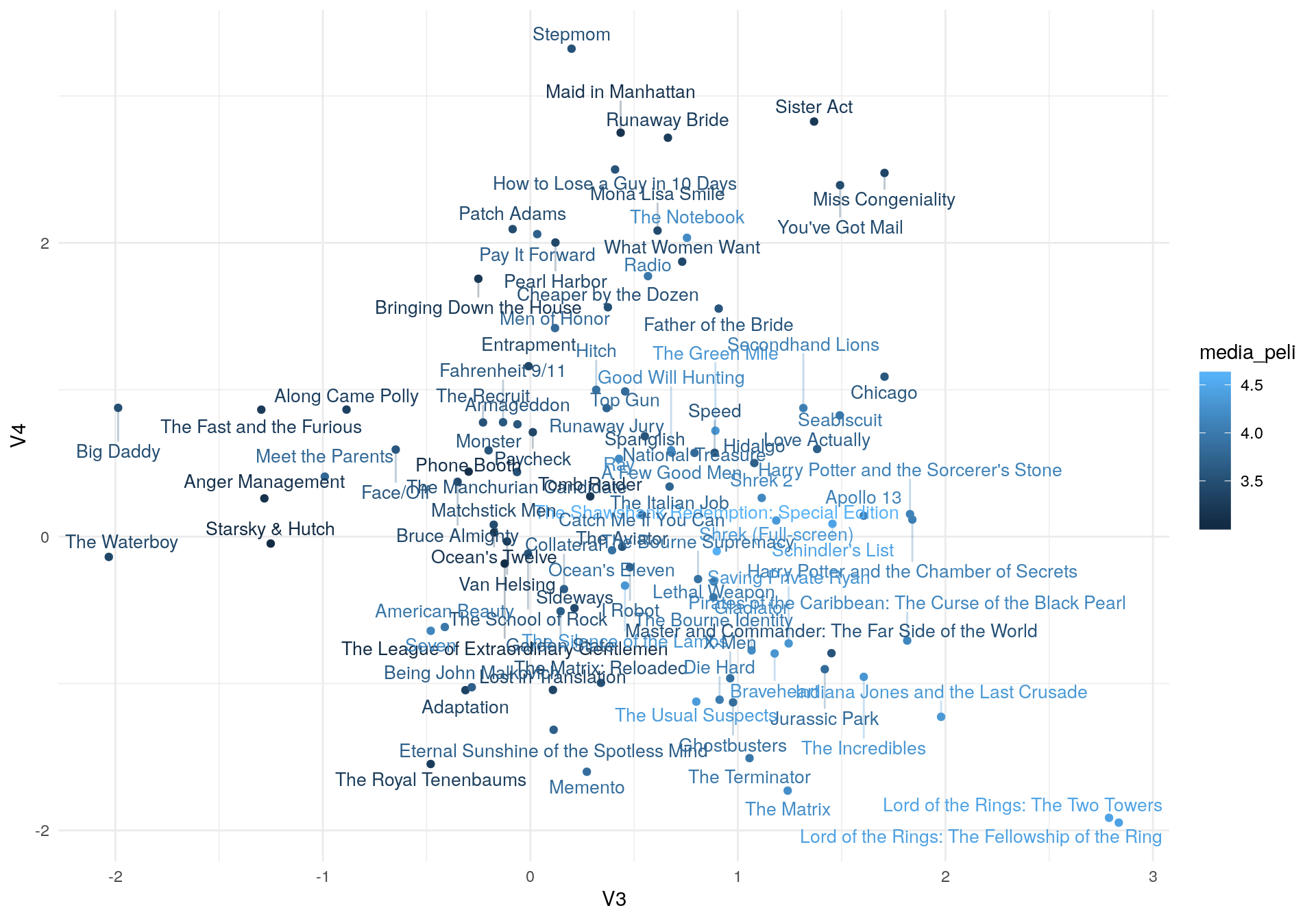
En la distribución de las películas en el espacio de dimensiones podemos apreciar el efecto del encogimiento:
## 0% 10% 20% 30% 40% 50% 60% 70% 80% 90% 100%
## 1 25 34 48 74 118 210 404 839 2578 48633ggplot(V_df, aes(x = V1, y= V2, label=nombre)) +
geom_point(alpha=0.5, size=0.5) + facet_wrap(~ntile(num_calif_peli, 10)) 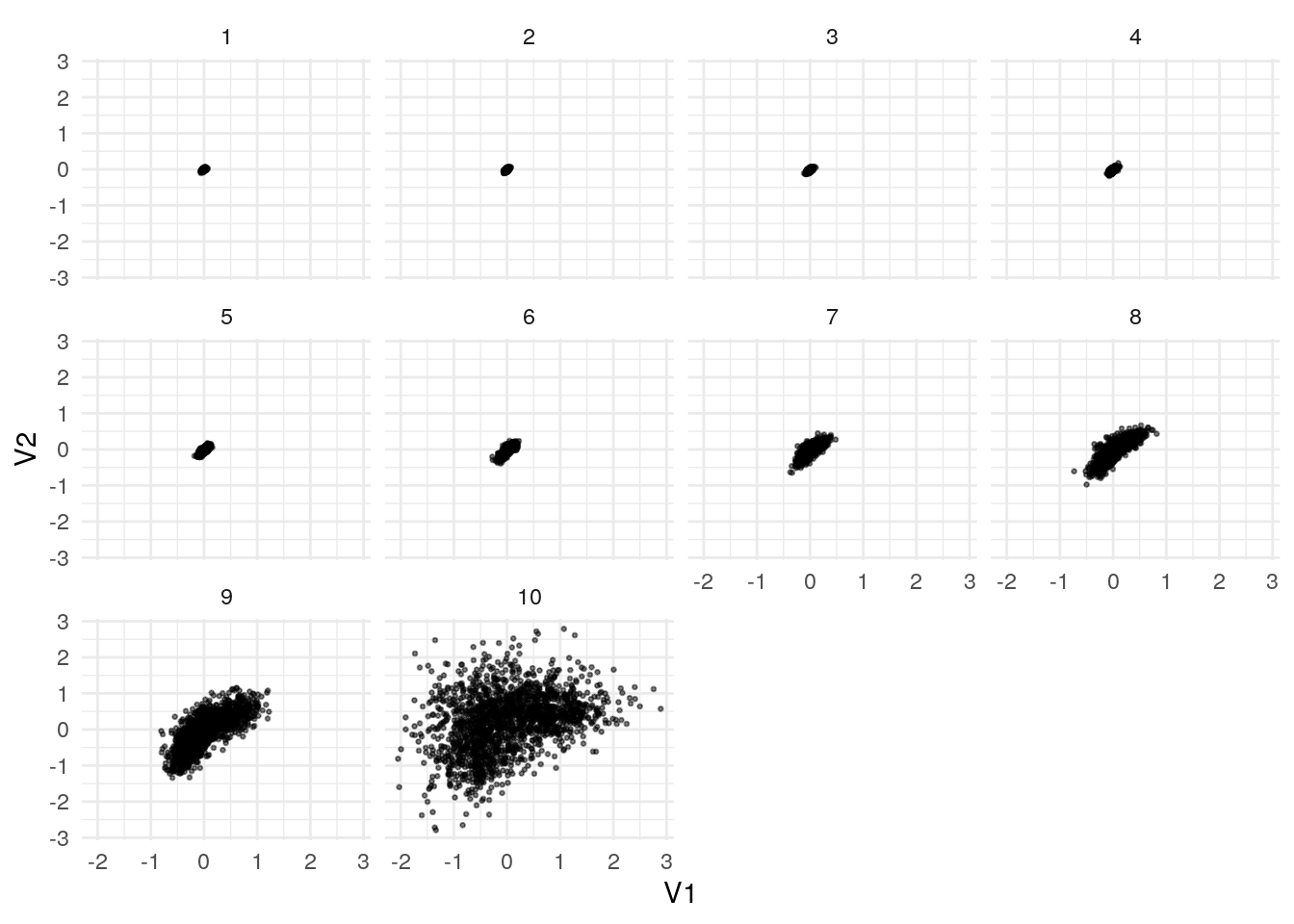
5.10 Más acerca del concurso de Netflix
Para tener desempeño equivalente los ganadores del concurso de Netflix (Koren, Bell, and Volinsky 2009), todavía faltan algunos elementos:
- A partir de \(2004\), hubo mejoras a la interfaz de Netflix. Esto provocó un incremento general en las calificaciones. Este es un factor (el tiempo), que es necesario incluir en el modelo como término adicional (si la calificación es antes o después del cambio).
En esta gráfica vemos el promedio local de las calificaciones conforme transcurre el tiempo:
##
## Attaching package: 'lubridate'## The following object is masked from 'package:base':
##
## dateggplot(sample_n(dat_entrena, 5000), aes(x= ymd(fecha), y = calif)) +
geom_smooth(method = 'loess', span=0.3)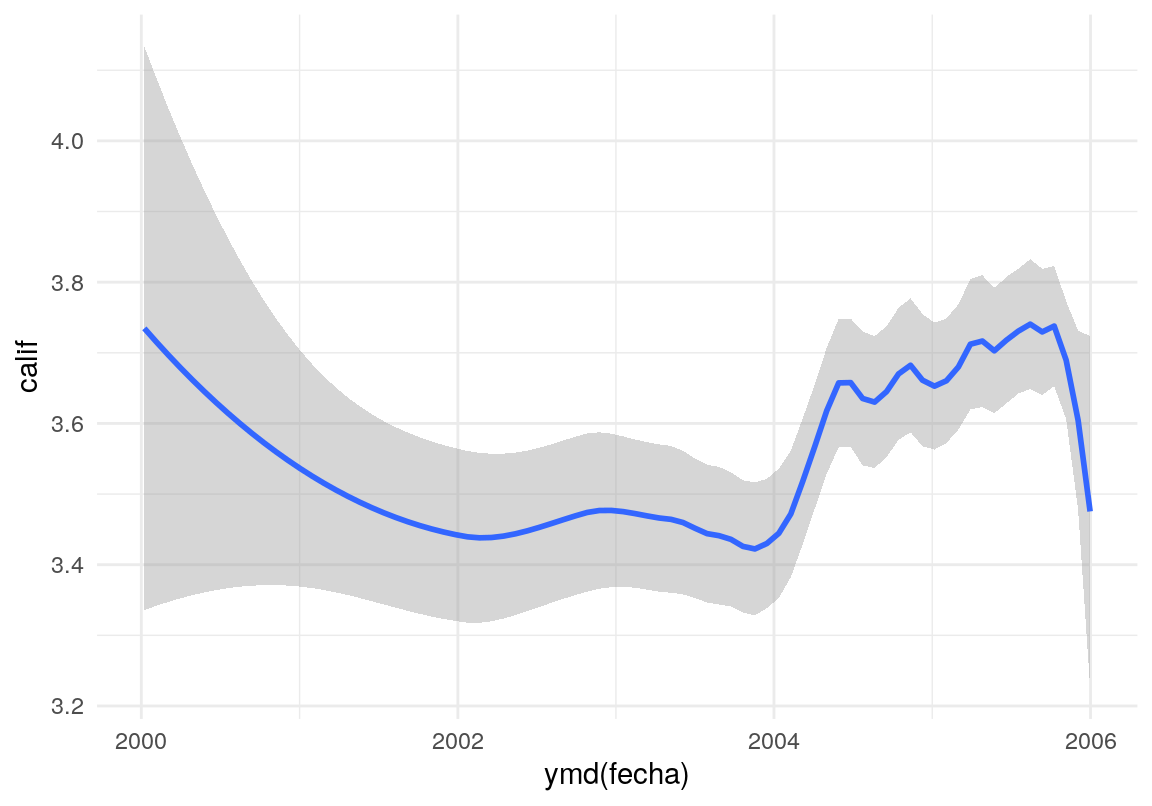
- Otro efecto, por ejemplo, es que películas más antiguas tienen calificaciones más altas (esto puede ser porque son las “sobreviven” en los catálogos).
ggplot(filter(medias_pelis, num_calif_peli > 1000),
aes(x = año, y = media_peli)) +
geom_point(alpha=0.4) + geom_smooth(method = 'loess', span=0.4)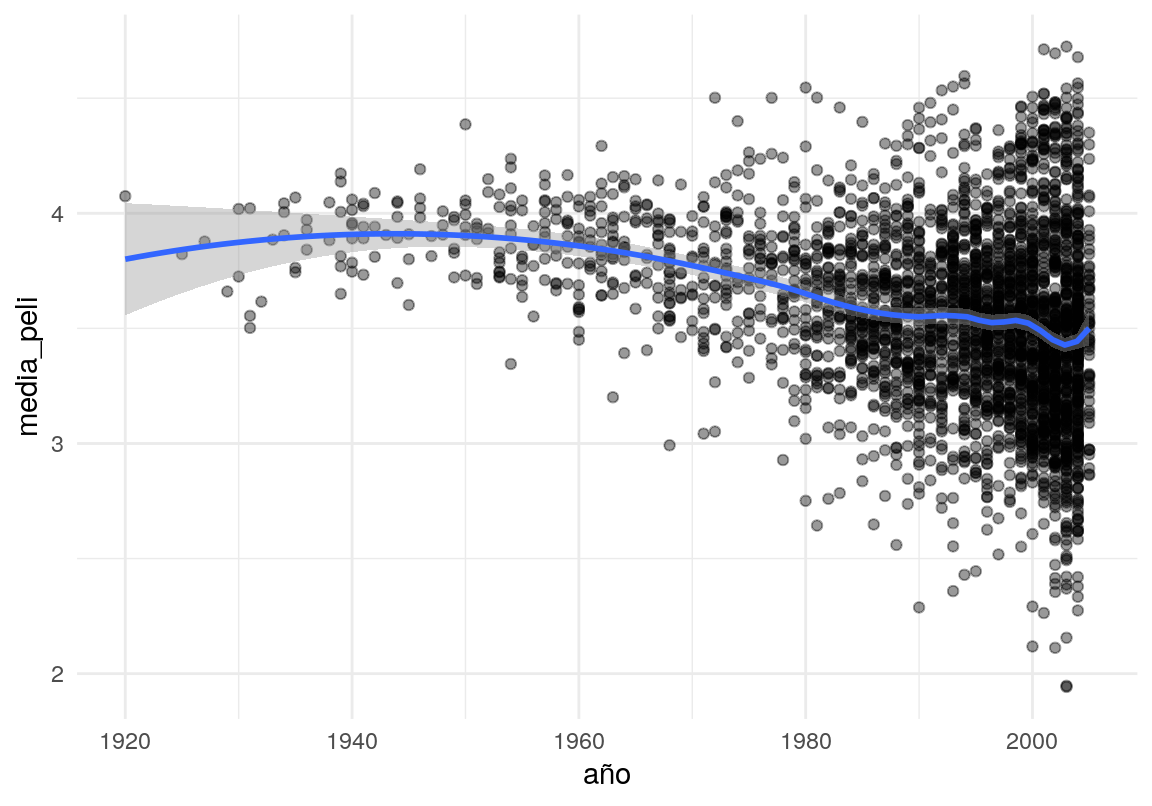
- Finalmente, el equipo ganador combinó varios métodos para mejorar la predicción (factores latentes, filtrado colaborativo, en varias versiones, y otros.
5.11 Retroalimentación implícita
Esta sección está basada en (Hu, Koren, and Volinsky 2008).
En el ejemplo que vimos arriba, la retroalimentación es expícita en el sentido de que los usuarios califican los artículos (\(1-\) no me gustó nada, hasta \(5-\) me gustó mucho). Sin embargo, es común encontrar casos donde no existe esta retroalimentación explícita, y solo tenemos medidas del gusto implícito, por ejemplo:
- Cuántas veces un usuario ha pedido un cierto artículo.
- Qué porcentaje del programa fue visto.
- Cuánto tiempo pasó en la página web.
- Cuántas veces oyó una canción.
Estos datos tienen la ventaja de que describen acciones del usuario, en lugar de un rating que puede estar influido por sesgos de imagen o de la calificación que “debería” tener un artículo además de la preferencia: quizá disfruto muchísimo Buffy the Vampire Slayer, pero lo califico con un \(3\), aunque un documental de ballenas que simplemente me gustó le pongo un \(5\). En los datos implícitos se vería de todas formas mi consumo frecuente de Buffy the Vampire Slayer, y quizá unos cuantos de documentales famosos.
Sea \(r_{ij}\) una medida implícita como las mencionadas arriba, para el usuario \(i\) y el artículo \(j\). Ponemos \(r_{i,j}=0\) cuando no se ha observado interacción entre este usuario y el artículo.
Una diferencia importante con los ratings explícitos es que los datos implícitos son en un sentido menos informativos que los explícitos:
Puede ser que el valor de \(r_{ij}\) sea relativamente bajo (pocas interacciones), pero de todas formas se trate de un artículo que es muy preferido (por ejemplo, solo vi Star Wars I una vez, pero me gusta mucho, o nunca he encontrado Star Wars I en el catálogo). Esto no pasa con los ratings, pues ratings bajos indican baja preferencia.
Sin embargo, estamos seguros de que niveles altos de interacción (oyó muchas veces una canción, etc.), es indicación de preferencia alta.
Usualmente la medida \(r_{ij}\) no tiene faltantes, o tiene un valor implícito para faltantes. Por ejemplo, si la medida es % de la película que vi, todas las películas con las que no he interactuado tienen \(r_{ij}=0\).
Así que en nuestro modelo no necesariamente queremos predecir directamente la variable \(r_{ij}\): puede haber artículos con predicción baja de \(r_{ij}\) que descubramos de todas formas van a ser altamente preferidos. Un modelo que haga una predicción de \(r_{îj}\) reflejaría más los patrones de consumo actual en lugar de permitirnos descubrir artículos preferidos con los que no necesariamente existe interacción.
5.11.1 Ejemplo
Consideremos los siguientes usuarios, donde medimos por ejemplo el número de minutos que pasó cada usuario viendo cada película:
imp <- tibble(usuario = 1:6,
StarWars1 = c(0, 0, 0, 150, 300, 250),
StarWars2 = c(5, 10, 0, 200, 220,180),
StarWars3 = c(200, 250, 300, 0, 0, 0))
imp## # A tibble: 6 x 4
## usuario StarWars1 StarWars2 StarWars3
## <int> <dbl> <dbl> <dbl>
## 1 1 0 5 200
## 2 2 0 10 250
## 3 3 0 0 300
## 4 4 150 200 0
## 5 5 300 220 0
## 6 6 250 180 0Quiséramos encontrar una manera de considerar los 0’s como información más suave (es decir, alguien puede tener valores bajos de interacción con una película, pero esto no implica necesariamente que no sea preferida). Esto implica que es más importante ajustar los valores altos del indicador implícito de preferencia.
Una solución propuesta en (Hu, Koren, and Volinsky 2008) (e implementada en spark) es darle menos importancia al valor \(r_{ij}\) en la construcción de los factores latentes, especialmente si tiene valores bajos.
Para hacer esto, primero definimos la variable de preferencia
\[p_{ij} = \begin{cases} 1, &\mbox{si } r_{ij}>0,\\ 0, &\mbox{si } r_{ij}=0.\\ \end{cases}\]
Esta variable \(p_{ij}\), cuando vale uno, indica algún nivel de preferencia. ¿Pero qué tanto valor debemos darle a esta preferencia? Definimos la confianza como \[c_{ij} = 1+ \alpha r_{ui},\] donde \(\alpha\) es un parámetro que hay que afinar (por ejemplo \(\alpha\) entre \(1\) y \(50\)). Para predicciones de vistas de TV, en (Hu, Koren, and Volinsky 2008) utilizan \(\alpha = 40\), donde \(r_{ij}\) es el número de veces que el usuario ha visto un programa (contando vistas parciales, así que es un número real).
La función objetivo (sin regularización) se define como
\[\begin{equation} L = \sum_{(i,j)} c_{ij}(p_{ij} - \sum_{l=1}^k u_{i,l}v_{j,l})^2 \tag{5.3} \end{equation}\]
Nótese que cuando \(c_ij\) es alta (porque \(r_{i,j}\) es alta), para minimizar esta cantidad tenemos que hacer la predicción cercana a 1, pues el error se multiplica por \(c_{ij}\). Sin embargo, cuando \(r_{i,j}\) es bajo, no es tan importante ajustar esta información con precisión: si \(p_{ij} = 1\), puede ser que \(\sum_{l=1}^k u_{i,l}v_{j,l}\) sea muy bajo, y si \(p_{ij}=0\), puede ser que \(\sum_{l=1}^k u_{i,l}v_{j,l}\) sea cercano a 1 sin afectar tanto el error.
5.11.2 Ejemplo
Veamos cómo se ven soluciones de un factor
imp_mat <- imp %>% select(-usuario) %>% as.matrix
error_explicito <- function(uv){
u <- matrix(uv[1:6], ncol = 1)
v <- matrix(uv[7:9], ncol = 1)
sum((imp_mat - u %*% t(v))^2)
}
error_implicito <- function(uv){
u <- matrix(uv[1:6], ncol = 1)
v <- matrix(uv[7:9], ncol = 1)
pref_mat <- as.numeric(imp_mat > 0) - u %*% t(v)
confianza <- 1 + 10 * imp_mat
sum(confianza * pref_mat^2 )
}Si intentamos ajustar los ratings impllícitos como si fueran explícitos, obtenemos los siguientes ajustados con un solo factor latente:
uv_inicial <- runif(9)
opt_exp <- optim(par = uv_inicial, error_explicito, method = "BFGS")
opt_exp$par[7:9]## [1] 21.1934667 17.5231521 0.6189195## [,1] [,2] [,3]
## [1,] 6 5 0
## [2,] 9 8 0
## [3,] 5 4 0
## [4,] 187 155 5
## [5,] 286 237 8
## [6,] 237 196 7Nótese que esta solución no es muy buena: una componente intenta capturar los patrones de consumo de estas tres películas.
Si usamos preferencias y confianza, obtenemos:
## [1] 1.288146 1.288696 1.296244## [,1] [,2] [,3]
## [1,] 0.99 0.99 1.00
## [2,] 0.99 0.99 1.00
## [3,] 0.99 0.99 1.00
## [4,] 1.00 1.00 1.01
## [5,] 1.00 1.00 1.01
## [6,] 1.00 1.00 1.01que indica que la información en esta matriz es consistente con que todos los usuarios tienen preferencia alta por las tres películas.
Igual que en los ejemplos anteriores, usualmente se agregan términos de regularización para los vectores renglón \(u_i\) y \(v_j\).
5.11.3 Evaluación para modelos implícitos
La evaluación para modelos implícitos no es tan simple como en el caso explícito, pues no estamos modelando directamente los valores observados \(r_{ij}\). Medidas como RECM o MAD que usamos en el caso explícito no son tan apropiadas para este problema.
Una alternativa es, para cada usuario \(i\), ordenar los artículos de mayor a menor valor de \(\hat{p}_{ij} = u_iv_j^t\) (canciones, pellículas), y calcular
\[ rank = \frac{\sum_{j} p_{ij}rank_{i,j}}{\sum_j p_{ij}} \]
donde \(rank_{ij}\) es el percentil del artículo \(j\) en la lista ordenada de artículos. \(rank_{ij}=0\) para el mejor artículo, y \(rank_{ij}=1\) para el peor. Es decir, obtenemos valores más bajos si observamos que los usuarios interactúan con artículos que están más arriba en el ranking.
Esta suma es un promedio sobre los rankings del usuario con \(p_{ij}=1\), y menores valores son mejores (quiere decir que hubo alguna preferencia por los items con \(rank_{ij}\) bajo, es decir, los mejores de nuestra lista predicha. Es posible también hacer un promedio ponderado por \(r_{ij}\): \[ rank = \frac{\sum_{j} r_{ij}rank_{i,j}}{\sum_j r_{ij}} \]
que es lo mismo que la ecuación anterior pero ponderando por el interés mostrado en cada artículo con \(p_{ij}=1\).
- Menores valores de \(rank\) son mejores.
- Si escogemos al azar el ordenamiento de los artículos, el valor esperado de \(rank_{ij}\) es \(0.5\) (en medio de la lista), lo que implica que el valor esperado de \(rank\) es \(0.50\). Cualquier modelo con \(rank\geq 0.5\) es peor que dar recomendaciones al azar.
Esta cantidad la podemos evaluar en entrenamiento y en validación. Para construir el conjunto de validación podemos hacer:
- Escogemos un número de usuarios para validación (por ejemplo \(20\%\))
- Ponemos \(50\%\) de los artículos evaluados por estas personas en validación, por ejemplo.
Estas cantidades dependen de cuántos datos tengamos, como siempre, para tener un tamaño razonable de datos de validación.
Referencias
Hu, Y., Y. Koren, and C. Volinsky. 2008. “Collaborative Filtering for Implicit Feedback Datasets.” In 2008 Eighth Ieee International Conference on Data Mining, 263–72. https://doi.org/10.1109/ICDM.2008.22.
Koren, Yehuda, Robert Bell, and Chris Volinsky. 2009. “Matrix Factorization Techniques for Recommender Systems.” Computer 42 (8). Los Alamitos, CA, USA: IEEE Computer Society Press: 30–37. https://doi.org/10.1109/MC.2009.263.
Leskovec, Jure, Anand Rajaraman, and Jeffrey David Ullman. 2014. Mining of Massive Datasets. 2nd ed. New York, NY, USA: Cambridge University Press. http://www.mmds.org.
Wickham, H. 2014. Advanced R. Chapman & Hall/Crc the R Series. Taylor & Francis. http://adv-r.had.co.nz.
Zhou, Yunhong, Dennis Wilkinson, Robert Schreiber, and Rong Pan. 2008. “Large-Scale Parallel Collaborative Filtering for the Netflix Prize.” In Algorithmic Aspects in Information and Management, edited by Rudolf Fleischer and Jinhui Xu, 337–48. Berlin, Heidelberg: Springer Berlin Heidelberg.